2011年广西梧州市中考数学试卷

试卷更新日期：2017-05-11 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣5的相反数是（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 在平面直角坐标系中，下面的点在第一象限的是（）

A、（1，2） B、（﹣2，3） C、（0，0） D、（﹣3，﹣2）

查看试题解析
3. 下列长度的三条线段能组成三角形的是（　　）

A、1，2，3 B、3，4，5 C、3，1，1 D、3，4，7

查看试题解析
4. 若一个菱形的一条边长为4cm，则这个菱形的周长为（　　）

A、20cm B、18cm C、16cm D、12cm

查看试题解析
5. 一组数据为：1，2，5，8，9，则这组数据的中位数是（　　）

A、2 B、5 C、8 D、9

查看试题解析
6. 因式分解x²y﹣4y的正确结果是（　　）

A、y（x+2）（x﹣2） B、y（x+4）（x﹣4） C、y（x²﹣4） D、y（x﹣2）²

查看试题解析
7. 如图，直线EO⊥CD，垂足为点O，AB平分∠EOD，则∠BOD的度数为（　　）

A、120° B、130° C、135° D、140°

查看试题解析
8. 不等式组的解集在数轴上表示为如图，则原不等式组的解集为（　　）

A、x＜2 B、x＜3 C、x≤3 D、x≤2

查看试题解析
9. 如图是从一幅扑克牌中取出的两组牌，分别是黑桃1，2，3，4红桃1，2，3，4，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌面数字之和等于7的概率是（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{8}$ C、 $\frac{1}{16}$ D、 $\frac{1}{32}$

查看试题解析
10.
如图，在平面直角坐标系中，直线y= $\frac{2}{3}$ x﹣ $\frac{2}{3}$ 与矩形ABCO的边OC、BC分别交于点E、F，已知OA=3，OC=4，则△CEF的面积是（　　）

A、6 B、3 C、12 D、 $\frac{4}{3}$

查看试题解析
11. 2011年5月22日﹣29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛．在比赛中，某次羽毛球的运动路线可以看作是抛物线y=﹣ $\frac{1}{4}$ x²+bx+c的一部分（如图），其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的解析式是（　　）

A、y=﹣ $\frac{1}{4}$ x²+ $\frac{3}{4}$ x+1 B、y=﹣ $\frac{1}{4}$ x²+ $\frac{3}{4}$ x﹣1 C、y=﹣ $\frac{1}{4}$ x²﹣ $\frac{3}{4}$ x+1 D、y=﹣ $\frac{1}{4}$ x²﹣ $\frac{3}{4}$ x﹣1

查看试题解析
12. 如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（　　）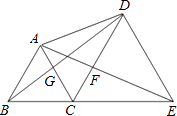

A、△ACE≌△BCD B、△BGC≌△AFC C、△DCG≌△ECF D、△ADB≌△CEA

查看试题解析

二、填空题

13. 如图，直线a、b相交，∠1=65°，则∠2的度数是°．

查看试题解析
14. 当a时， $\sqrt{a + 2}$ 在实数范围内一有意义．

查看试题解析
15. 一元二次方程x²+5x+6=0的根是．

查看试题解析
16. 如图，三个半径都为3cm的圆两两外切，切点分别为D、E、F，则EF的长为cm．

查看试题解析
17. 如图是由两个长方体组合而成的一个立体图形的三视图，根据图中所标尺寸（单位：mm），计算出这个立体图形的表面积是mm² ．

查看试题解析
18.
如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称或中心对称变换，若原来点A坐标是（a，b），则经过第2011次变换后所得的A点坐标是．

查看试题解析

三、解答题

19. 计算：|﹣ $\sqrt{2}$ |﹣ $\sqrt{8}$ +（3﹣π）⁰ ．

查看试题解析
20. 已知B（2，n）是正比例函数y=2x图象上的点．

(1)、求点B的坐标；

(2)、若某个反比例函数图象经过点B，求这个反比例函数的解析式．

查看试题解析
21. 在今年法国网球公开赛中，我国选手李娜在决赛中成功击败对手夺冠，称为获得法国网球公开赛冠军的亚洲第一人．某班体育委员就本班同学对该届法国网球公开赛的了解程度进行全面调查统计，收集数据后绘制了两幅不完整的统计图，如图（1）和图（2）．根据图中的信息，解答下列问题：

(1)、该班共有名学生；

(2)、在图（1）中，“很了解”所对应的圆心角的度数为；

(3)、把图（2）中的条形图形补充完整．

查看试题解析
22. 如图，在▱ABCD中，E为BC的中点，连接DE．延长DE交AB的延长线于点F．求证：AB=BF．

查看试题解析
23.
如图，某小区楼房附近有一个斜坡，小张发现楼房在水平地面与斜坡处形成的投影中，在斜坡上的影子长CD=6m，坡角到楼房的距离CB=8m．在D点处观察点A的仰角为54°，已知坡角为30°，你能求出楼房AB的高度吗？（tan54°≈1.38，结果精确到0.1m）

查看试题解析
24. 由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．

(1)、今年甲型号手机每台售价为多少元？

(2)、为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？

(3)、若乙型号手机的售价为1400元，为了促销，公司决定每售出一台乙型号手机，返还顾客现金a元，而甲型号手机仍按今年的售价销售，要使（2）中所有方案获利相同，a应取何值？

查看试题解析
25. 如图，AB是⊙O的直径，CD是⊙O的切线，切点为C．延长AB交CD于点E．连接AC，作∠DAC=∠ACD，作AF⊥ED于点F，交⊙O于点G．

(1)、求证：AD是⊙O的切线；

(2)、如果⊙O的半径是6cm，EC=8cm，求GF的长．

查看试题解析
26. 如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=6cm，AB=8cm，BC=14cm．动点P、Q都从点C出发，点P沿C→B方向做匀速运动，点Q沿C→D→A方向做匀速运动，当P、Q其中一点到达终点时，另一点也随之停止运动．

(1)、求CD的长；

(2)、若点P以1cm/s速度运动，点Q以2 $\sqrt{2}$ cm/s的速度运动，连接BQ、PQ，设△BQP面积为S（cm²），点P、Q运动的时间为t（s），求S与t的函数关系式，并写出t的取值范围；

(3)、若点P的速度仍是1cm/s，点Q的速度为acm/s，要使在运动过程中出现PQ∥DC，请你直接写出a的取值范围．

查看试题解析