2017年河北省石家庄市中考数学模拟试卷

试卷更新日期：2017-05-11 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的绝对值是（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 下列计算正确的是（）

A、3a+2a=6a B、a⁶÷a²=a⁴ C、a²+a³=a⁵ D、（a²）³=a⁵

查看试题解析
3. 下列四个图形中，既是轴对称图形又是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、正六边形 D、五角星

查看试题解析
4. 下列运算结果是x+1的是（）

A、 $\frac{x^{2} + 1}{x+1}$ B、 $\frac{1 - x^{2}}{x+1}$ C、 $\frac{x-1}{x^{2} -1}$ D、 $\frac{x^{2}}{x-1} + \frac{1}{1 - x}$

查看试题解析
5.
小红制作了一个正方体，其表面展开图如图所示，正方体中与“文”所对的面上的汉字应是（）

A、城 B、明 C、全 D、国

查看试题解析
6. 下列命题正确的是（）

A、对角线互相垂直的四边形是菱形 B、对角线相等且垂直的四边形是正方形 C、平行四边形的对角线互相平分 D、对角线相等的四边形是矩形

查看试题解析
7. 关于 $\sqrt{18}$ 的叙述错误的是（）

A、它是一个无限不循环小数 B、它在3和4之间 C、它化简后为3 $\sqrt{2}$ D、以它为直径的圆的面积是 $\frac{9}{2}$ π

查看试题解析
8. 在反比例函数y= $\frac{1 - 3 m}{x}$ 图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），若x₁＜x₂＜0，y₁＜y₂ ，则m的取值范围是（）

A、m $> \frac{1}{3}$ B、m $< \frac{1}{3}$ C、m $\geq \frac{1}{3}$ D、m $\leq \frac{1}{3}$

查看试题解析
9. 如图，下列结论正确的个数是（）
①m+n＞0；②m﹣n＞0；③mn＜0；④|m﹣n|=m﹣n．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，点F是△ABC的内心，∠A=50°，则∠BFC=（）

A、100° B、115° C、130° D、135°

查看试题解析
11. 数学课上，小丽用尺规这样作图：（1），以点O为圆心，任意长为半径作弧，交OA，OB于D，E两点；（2）分别以点D，E为圆心，大于 $\frac{1}{2}$ DE的长为半径作弧，两弧交于点C；第三部，作射线OC并连接CD，CE，下列结论不正确的是（）

A、∠1=∠2 B、S_△_OCE=S_△_OCD C、OD=CD D、OC垂直平分DE

查看试题解析
12. 为弘扬中华传统诗词文化，营造书香校园文化氛围，某校初二年级组织了“书香校园之中华好诗词大赛”，琪琪根据比赛中七位评委所给的某位参赛选手的分数，制作了一个表格（见表），如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（）
中位数
众数
平均数
方差
9.1
9.2
9.1
0.2

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
13. 下列三个三角形中相似的是（）

A、A与B B、A与C C、B与C D、A，B，C都相似

查看试题解析
14. 如图，这是2016年12月的日历表，任意圈出一竖列上相邻的四个数，请你运用方程的思想来研究，发现这四个数的和不可能是（）

A、50 B、58 C、68 D、70

查看试题解析
15. 常数a，b，c在数轴上的位置如图所示，则关于x的一元二次方程ax²+bx+c=0根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定

查看试题解析
16. 如图，在矩形ABCD中，AB=8 $\sqrt{3}$ ，AD=10，点E是CD的中点，将这张纸片依次折叠两次：第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则下列结论正确的个数是（）
①ME∥HG；②△MEH是等边三角形；③∠EHG=∠AMN；④tan∠EHG= $\frac{5 \sqrt{3}}{6}$

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

17. 27的立方根为．

查看试题解析
18. 若a²=a+2，则2a²﹣2a+2017的值为．

查看试题解析
19. 如图，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转90°，点A，C分别落在点A′、C′处，并且点A′，C′，B在同一条直线上，则tan∠ABA′的值为．

查看试题解析
20.
如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l₁ ， l₂ ，过点（1，0）作x轴的垂线交l₁于点A₁ ，过点A₁作y轴的垂线交l₂于点A₂ ，过点A₂作x轴的垂线交l₁于点A₃ ，过点A₃作y轴的垂线交l₂于点A₄ ， …依次进行下去，则点A₂₀₁₇的坐标为．

查看试题解析

三、解答题

21. 观察下图回答问题：

(1)、指出小明的作业从哪一步开始出现的错误，请更正过来，并计算出正确结果；

(2)、若a，b是不等式组 ${\begin{matrix} 2 x > 0 \\ x-3 < 0 \end{matrix}$ 的整数解（a＜b），求上题{}分式的值．

查看试题解析
22. 已知：∠ACB=90°，AC=BC，AD⊥CM，BE⊥CM，垂足分别为D，E，

(1)、如图1，
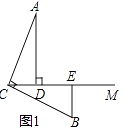
①线段CD和BE的数量关系是；
②请写出线段AD，BE，DE之间的数量关系．

(2)、如图2，上述结论②还成立吗？如果不成立，请直接写出线段AD，BE，DE之间的数量关系．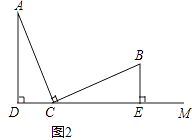

查看试题解析
23. 如图，放在平面直角坐标系中的圆O的半径为3，现做如下实验：抛掷一枚均匀的正四面体骰子，它有四个顶点，各顶点数分别是1，2，3，4，每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的点数作为直角坐标系中点P的坐标（第一次的点数为横坐标，第二次的点数为纵坐标）．

(1)、若第一次骰子朝上的点数为1，第二次骰子朝上的点数为2，此时点P（填“是”或“否”）落在圆O内部；

(2)、请你用树状图或列表的方法表示出P点坐标的所有可能结果；

(3)、求点P落在圆O面上（含内部与边界）的概率．

查看试题解析
24. 甲、乙两列火车分别从A，B两城同时相向匀速驶出，甲车开往终点B城，乙车开往终点A城，乙车比甲车早到达终点；如图，是两车相距的路程d（千米）与行驶时间t（小时）的函数关系图象．

(1)、A，B两城相距千米，经过小时两车相遇；

(2)、分别求出甲、乙两车的速度；

(3)、直接写出甲车距A城的路程S₁、乙车距A城的路程S₂与t的函数关系式；（不必写出t的范围）

(4)、当两车相距100千米时，求t的值．

查看试题解析
25. 如图，△ABC中，∠ACB=90°，∠ABC=45°，BC=12cm，半圆O的直径DE=12cm，点E与点C重合，半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在BC所在的直线上．设运动时间为x（s），半圆O在△ABC的重叠部分的面积为S（cm²）．

(1)、当x=（s）时，点O与线段BC的中点重合；

(2)、在（1）的条件下，求半圆O与△ABC的重叠部分的面积S；

(3)、当x为何值时，半圆O所在的圆与△ABC的边所在的直线相切？

查看试题解析
26.
如图，在平面直角坐标系中，已知抛物线y=ax²+bx﹣8与x轴交于两点A，B，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为点D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（﹣2，0），（6，﹣8）．

(1)、求抛物线的函数表达式；

(2)、求点E的坐标；

(3)、试探究在x轴下方的抛物线上是否存在点F，使得△FOB和△EOB的面积相等，若存在，请求出点F的坐标，若不存在，请说明理由；

(4)、若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点Q，请直接写出：当m为何值时，△OPQ是等腰三角形．

查看试题解析

中位数	众数	平均数	方差
9.1	9.2	9.1	0.2