2013年四川省绵阳市中考数学试卷

试卷更新日期：2017-05-11 类型：中考真卷

进入出卷网下载

一、选择题：

1. $\sqrt{2}$ 的相反数是（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、﹣ $\sqrt{2}$ D、﹣ $\frac{\sqrt{2}}{2}$

查看试题解析
2. 下列“数字”图形中，有且仅有一条对称轴的是（）

A、 B、 C、 D、

查看试题解析
3. 2013年，我国上海和安徽首先发现“H7N9”禽流感，H7N9是一种新型禽流感，其病毒颗粒呈多形性，其中球形病毒的最大直径为0.00000012米，这一直径用科学记数法表示为（）

A、1.2×10^﹣⁹米 B、1.2×10^﹣⁸米 C、12×10^﹣⁸米 D、1.2×10^﹣⁷米

查看试题解析
4. 设“▲”、“●”、“■”分别表示三种不同的物体，现用天平秤两次，情况如图所示，那么▲、●、■这三种物体按质量从大到小排列应为（）

A、■、●、▲ B、▲、■、● C、■、▲、● D、●、▲、■

查看试题解析
5. 把如图中的三棱柱展开，所得到的展开图是（）

A、 B、 C、 D、

查看试题解析
6. 下列说法正确的是（）

A、对角线相等且互相垂直的四边形是菱形 B、对角线互相垂直的梯形是等腰梯形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形

查看试题解析
7. 如图，要拧开一个边长为a=6mm的正六边形螺帽，扳手张开的开口b至少为（）

A、6 $\sqrt{2}$ mm B、12mm C、6 $\sqrt{3}$ mm D、4 $\sqrt{3}$ mm

查看试题解析
8. 朵朵幼儿园的阿姨给小朋友分苹果，如果每人3个还少3个，如果每人2个又多2个，请问共有多少个小朋友？（）

A、4个 B、5个 C、10个 D、12个

查看试题解析
9.
如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底点G为BC的中点，则矮建筑物的高CD为（）

A、20米 B、10 $\sqrt{3}$ 米 C、15 $\sqrt{3}$ 米 D、5 $\sqrt{6}$ 米

查看试题解析
10. 如图，四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，且DH与AC交于G，则GH=（）

A、 $\frac{28}{25}$ cm B、 $\frac{21}{20}$ cm C、 $\frac{28}{15}$ cm D、 $\frac{25}{21}$ cm

查看试题解析
11. “服务他人，提升自我”，七一学校积极开展志愿者服务活动，来自初三的5名同学（3男两女）成立了“交通秩序维护”小分队，若从该小分队中任选两名同学进行交通秩序维护，则恰好是一男一女的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
12. 把所有正奇数从小到大排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，现用等式A_M=（i，j）表示正奇数M是第i组第j个数（从左往右数），如A₇=（2，3），则A₂₀₁₃=（）

A、（45，77） B、（45，39） C、（32，46） D、（32，23）

查看试题解析

二、填空题：

13. 因式分解：x²y⁴﹣x⁴y²= ．

查看试题解析
14. 如图，AC、BD相交于O，AB∥DC，AB=BC，∠D=40°，∠ACB=35°，则∠AOD= ．

查看试题解析
15.
如图，把“QQ”笑脸放在直角坐标系中，已知左眼A的坐标是（﹣2，3），嘴唇C点的坐标为（﹣1，1），则将此“QQ”笑脸向右平移3个单位后，右眼B的坐标是．

查看试题解析
16. 对正方形ABCD进行分割，如图1，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分化线可以剪出一副“七巧板”，用这些部件可以拼出很多图案，图2就是用其中6块拼出的“飞机”．若△GOM的面积为1，则“飞机”的面积为．

查看试题解析
17. 已知整数k＜5，若△ABC的边长均满足关于x的方程x²﹣3 $\sqrt{k}$ x+8=0，则△ABC的周长是．

查看试题解析
18. 二次函数y=ax²+bx+c的图象如图所示，给出下列结论：
①2a+b＞0；②b＞a＞c；③若﹣1＜m＜n＜1，则m+n＜﹣ $\frac{b}{a}$ ；④3|a|+|c|＜2|b|．
其中正确的结论是（写出你认为正确的所有结论序号）．

查看试题解析

三、解答题：

19.

(1)、计算： $- 2^{- 2} + | 1 - \frac{1}{\sin 45^{\circ}} | \times (\sqrt{8} + 2)$ ；

(2)、解方程： $\frac{x}{x - 1} - 1 = \frac{3}{x^{2} + x - 2}$ ．

查看试题解析
20. 为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表：
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图

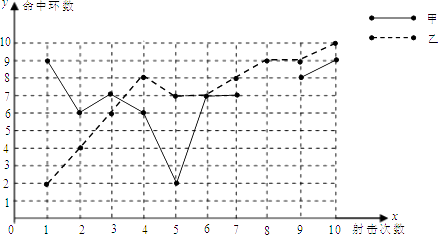(1)、请补全上述图表（请直接在表中填空和补全折线图）；

(2)、如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；

(3)、如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？

查看试题解析
21. 如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．

(1)、判断CD与⊙O的位置关系，并证明你的结论；

(2)、若E是 $\hat{A C}$ 的中点，⊙O的半径为1，求图中阴影部分的面积．

查看试题解析
22.
如图，已知矩形OABC中，OA=2，AB=4，双曲线 $y = \frac{k}{x}$ （k＞0）与矩形两边AB、BC分别交于E、F．

(1)、若E是AB的中点，求F点的坐标；

(2)、若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值．

查看试题解析
23. “低碳生活，绿色出行”，自行车正逐渐成为人们喜爱的交通工具．某运动商城的自行车销售量自2013年起逐月增加，据统计，该商城1月份销售自行车64辆，3月份销售了100辆．

(1)、若该商城前4个月的自行车销量的月平均增长率相同，问该商城4月份卖出多少辆自行车？

(2)、考虑到自行车需求不断增加，该商城准备投入3万元再购进一批两种规格的自行车，已知A型车的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆．根据销售经验，A型车不少于B型车的2倍，但不超过B型车的2.8倍．假设所进车辆全部售完，为使利润最大，该商城应如何进货？

查看试题解析
24.
如图，二次函数y=ax²+bx+c的图象的顶点C的坐标为（0，﹣2），交x轴于A、B两点，其中A（﹣1，0），直线l：x=m（m＞1）与x轴交于D．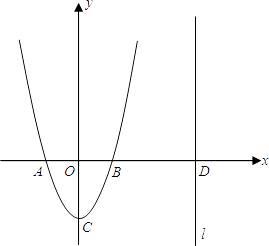

(1)、求二次函数的解析式和B的坐标；

(2)、在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；

(3)、在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由．

查看试题解析
25.
我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题．请你利用重心的概念完成如下问题：

(1)、若O是△ABC的重心（如图1），连结AO并延长交BC于D，证明： $\frac{A O}{A D} = \frac{2}{3}$ ；

(2)、若AD是△ABC的一条中线（如图2），O是AD上一点，且满足 $\frac{A O}{A D} = \frac{2}{3}$ ，试判断O是△ABC的重心吗？如果是，请证明；如果不是，请说明理由；

(3)、若O是△ABC的重心，过O的一条直线分别与AB、AC相交于G、H（均不与△ABC的顶点重合）（如图3），S_四边形_BCHG ， S_△_AGH分别表示四边形BCHG和△AGH的面积，试探究 $\frac{S_{四边形 B C H G}}{S_{△ A G H}}$ 的最大值．

查看试题解析

	平均数	中位数	方差	命中10环的次数
甲	7			0
乙				1