2013年四川省成都市中考数学试卷

试卷更新日期：2017-05-11 类型：中考真卷

进入出卷网下载

一、选择题

1. 2的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 如图所示的几何体的俯视图可能是（）

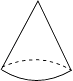A、 B、 C、 D、

查看试题解析
3. 要使分式 $\frac{5}{x - 1}$ 有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x＜1 D、x≠﹣1

查看试题解析
4. 如图，在△ABC中，∠B=∠C，AB=5，则AC的长为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列运算正确的是（）

A、 $\frac{1}{3}$ ×（﹣3）=1 B、5﹣8=﹣3 C、2^﹣³=6 D、（﹣2013）⁰=0

查看试题解析
6. 参加成都市今年初三毕业会考的学生约有13万人，将13万用科学记数法表示应为（）

A、1.3×10⁵ B、13×10⁴ C、0.13×10⁵ D、0.13×10⁶

查看试题解析
7. 如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 在平面直角坐标系中，下列函数的图象经过原点的是（）

A、y=﹣x+3 B、y= $\frac{5}{x}$ C、y=2x D、y=﹣2x²+x﹣7

查看试题解析
9. 一元二次方程x²+x﹣2=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
10. 如图，点A，B，C在⊙O上，∠A=50°，则∠BOC的度数为（）

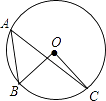A、40° B、50° C、80° D、100°

查看试题解析

二、填空题

11. 不等式2x﹣1＞3的解集是．

查看试题解析
12. 今年4月20日在雅安市芦山县发生了7.0级的大地震，全川人民众志成城，抗震救灾．某班组织“捐零花钱，献爱心”活动，全班50名学生的捐款情况如图所示，则本次捐款金额的众数是元．

查看试题解析
13. 如图，∠B=30°，若AB∥CD，CB平分∠ACD，则∠ACD=度．

查看试题解析
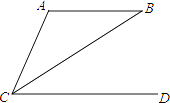14.
如图，某山坡的坡面AB=200米，坡角∠BAC=30°，则该山坡的高BC的长为米．

查看试题解析

三、解答题

15.

(1)、计算： ${(- 2)}^{2} + | - \sqrt{3} | + 2 \sin 60^{\circ} - \sqrt{12}$

(2)、解方程组： ${\begin{matrix} x + y = 1 \\ 2 x - y = 5 \end{matrix}$ ．

查看试题解析
16. 化简 $(a^{2} - a) \div \frac{a^{2} - 2 a + 1}{a - 1}$ ．

查看试题解析
17. 如图，在边长为1的小正方形组成的方格纸上，将△ABC绕着点A顺时针旋转90°

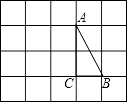(1)、画出旋转之后的△AB′C′；

(2)、求线段AC旋转过程中扫过的扇形的面积．

查看试题解析
18. “中国梦”关乎每个人的幸福生活，为进一步感知我们身边的幸福，展现成都人追梦的风采，我市某校开展了以“梦想中国，逐梦成都”为主题的摄影大赛，要求参赛学生每人交一件作品．现将参赛的50件作品的成绩（单位：分）进行统计如下：
等级
成绩（用s表示）
频数
频率
A
90≤s≤100
x
0.08
B
80≤s＜90
35
y
C
s＜80
11
0.22
合计
50
1
请根据上表提供的信息，解答下列问题：

(1)、表中的x的值为， y的值为

(2)、将本次参赛作品获得A等级的学生依次用A₁ ， A₂ ， A₃ ， …表示，现该校决定从本次参赛作品中获得A等级学生中，随机抽取两名学生谈谈他们的参赛体会，请用树状图或列表法求恰好抽到学生A₁和A₂的概率．

查看试题解析
19. 如图，一次函数y₁=x+1的图象与反比例函数 $y_{2} = \frac{k}{x}$ （k为常数，且k≠0）的图象都经过点A（m，2）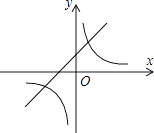

(1)、求点A的坐标及反比例函数的表达式；

(2)、结合图象直接比较：当x＞0时，y₁和y₂的大小．

查看试题解析
20. 如图，点B在线段AC上，点D、E在AC同侧，∠A=∠C=90°，BD⊥BE，AD=BC．

(1)、求证：AC=AD+CE；

(2)、若AD=3，CE=5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q；
（i）当点P与A、B两点不重合时，求 $\frac{D P}{P Q}$ 的值；
（ii）当点P从A点运动到AC的中点时，求线段DQ的中点所经过的路径（线段）长．（直接写出结果，不必写出解答过程）

查看试题解析

四、填空题

21. 已知点（3，5）在直线y=ax+b（a，b为常数，且a≠0）上，则 $\frac{a}{b - 5}$ 的值为．

查看试题解析
22. 2013•成都）若正整数n使得在计算n+（n+1）+（n+2）的过程中，各数位均不产生进位现象，则称n为“本位数”．例如2和30是“本位数”，而5和91不是“本位数”．现从所有大于0且小于100的“本位数”中，随机抽取一个数，抽到偶数的概率为．

查看试题解析
23. 若关于t的不等式组 ${\begin{matrix} t - a \geq 0 \\ 2 t + 1 \leq 4 \end{matrix}$ ，恰有三个整数解，则关于x的一次函数 $y = \frac{1}{4} x - a$ 的图象与反比例函数 $y = \frac{3 a + 2}{x}$ 的图象的公共点的个数为．

查看试题解析
24. 在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线y= $\frac{1}{3}$ x²﹣2交于A，B两点，且A点在y轴左侧，P点的坐标为（0，﹣4），连接PA，PB．有以下说法：
①PO²=PA•PB；
②当k＞0时，（PA+AO）（PB﹣BO）的值随k的增大而增大；
③当k=- $\frac{\sqrt{3}}{3}$ 时，BP²=BO•BA；
④△PAB面积的最小值为 $4 \sqrt{6}$ ．
其中正确的是．（写出所有正确说法的序号）

查看试题解析
25. 如图，A，B，C为⊙O上相邻的三个n等分点， $\hat{A B} = \hat{B C}$ ，点E在 $\hat{B C}$ 上，EF为⊙O的直径，将⊙O沿EF折叠，使点A与A′重合，点B与B′重合，连接EB′，EC，EA′．设EB′=b，EC=c，EA′=p．现探究b，c，p三者的数量关系：发现当n=3时，p=b+c．请继续探究b，c，p三者的数量关系：当n=4时，p=；当n=12时，p= ．
（参考数据：sin15°=cos75°= $\frac{\sqrt{6} - \sqrt{2}}{4}$ ，cos15°=sin75°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ ）

查看试题解析

五、解答题

26. 某物体从P点运动到Q点所用时间为7秒，其运动速度v（米每秒）关于时间t（秒）的函数关系如图所示．某学习小组经过探究发现：该物体前进3秒运动的路程在数值上等于矩形AODB的面积．由物理学知识还可知：该物体前t（3＜t≤7）秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和．
根据以上信息，完成下列问题：

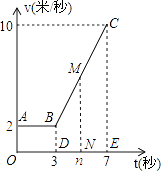(1)、当3＜t≤7时，用含t的式子表示v；

(2)、分别求该物体在0≤t≤3和3＜t≤7时，运动的路程s（米）关于时间t（秒）的函数关系式；并求该物体从P点运动到Q总路程的 $\frac{7}{10}$ 时所用的时间．

查看试题解析
27. 如图，⊙O的半径r=25，四边形ABCD内接于圆⊙O，AC⊥BD于点H，P为CA延长线上的一点，且∠PDA=∠ABD．

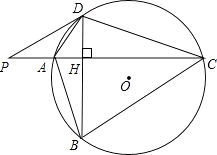(1)、试判断PD与⊙O的位置关系，并说明理由；

(2)、若tan∠ADB= $\frac{3}{4}$ ，PA= $\frac{4 \sqrt{3} - 3}{3}$ AH，求BD的长；

(3)、在（2）的条件下，求四边形ABCD的面积．

查看试题解析
28.
在平面直角坐标系中，已知抛物线y= $- \frac{1}{2}$ x²+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．

(1)、如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

(2)、平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．
（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；
（ii）取BC的中点N，连接NP，BQ．试探究 $\frac{P Q}{N P + B Q}$ 是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

查看试题解析

等级	成绩（用s表示）	频数	频率
A	90≤s≤100	x	0.08
B	80≤s＜90	35	y
C	s＜80	11	0.22
合计		50	1