2012年四川省内江市中考数学试卷
试卷更新日期:2017-05-11 类型:中考真卷
一、选择题
-
1. ﹣6的相反数为( )A、6 B、 C、- D、﹣62. 下列计算正确的是( )A、a2+a4=a6 B、2a+3b=5ab C、(a2)3=a6 D、a6÷a3=a23. 已知反比例函数 的图象经过点(1,﹣2),则k的值为( )A、2 B、- C、1 D、﹣24. 下列图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个5. 如图,a∥b,∠1=65°,∠2=140°,则∠3=( )
A、4个 B、3个 C、2个 D、1个5. 如图,a∥b,∠1=65°,∠2=140°,则∠3=( ) A、100° B、105° C、110° D、115°6. 一组数据4,3,6,9,6,5的中位数和众数分别是( )A、5和5.5 B、5.5和6 C、5和6 D、6和67. 函数 的图象在( )A、第一象限 B、第一、三象限 C、第二象限 D、第二、四象限8.
A、100° B、105° C、110° D、115°6. 一组数据4,3,6,9,6,5的中位数和众数分别是( )A、5和5.5 B、5.5和6 C、5和6 D、6和67. 函数 的图象在( )A、第一象限 B、第一、三象限 C、第二象限 D、第二、四象限8.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD= ,则阴影部分图形的面积为( )
 A、4π B、2π C、π D、9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=10,BC=5,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为( )
A、4π B、2π C、π D、9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=10,BC=5,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为( ) A、15 B、20 C、25 D、3011. 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A、15 B、20 C、25 D、3011. 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )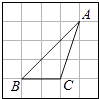 A、 B、 C、 D、12.
A、 B、 C、 D、12.如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致为( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 分解因式:ab3﹣4ab= .14. 由一些大小相同的小正方形组成的一个几何体的主视图和俯视图如图所示,那么组成该几何体所需的小正方形的个数最少为 .
 15. 如图所示,A、B是边长为1的小正方形组成的网格的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是 .
15. 如图所示,A、B是边长为1的小正方形组成的网格的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是 .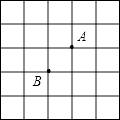 16. 如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD= .
16. 如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD= .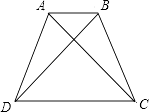
三、解答题
-
17. 计算: .18.
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
 (1)、已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)、求加固后的大坝背水坡面DE的坡度.19. 某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)、已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)、求加固后的大坝背水坡面DE的坡度.19. 某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:造型花卉
甲
乙
A
80
40
B
50
70
(1)、符合题意的搭配方案有几种?(2)、如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?20. 某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
 (1)、求出样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.21. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.
(1)、求出样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.21. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F. (1)、求证:四边形ABCD是正方形;(2)、当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论.
(1)、求证:四边形ABCD是正方形;(2)、当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论.四、填空题
-
22. 已知三个数x,y,z,满足 ,则 = .23.
已知反比例函数 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1 , M2 , M3…,Mn , 则 = .
 24. 已知ai≠0(i=1,2,…,2012)满足 ,使直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限的ai概率是 .25. 已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为 .
24. 已知ai≠0(i=1,2,…,2012)满足 ,使直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限的ai概率是 .25. 已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为 .五、解答题
-
26.
已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
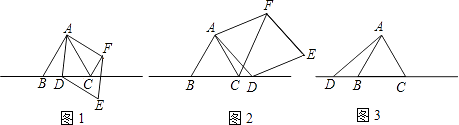 (1)、如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)、如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)、如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.27. 如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1•x2=q,请根据以上结论,解决下列问题:(1)、已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;(2)、已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 的值;(3)、已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.28.
(1)、如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)、如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)、如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.27. 如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1•x2=q,请根据以上结论,解决下列问题:(1)、已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;(2)、已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 的值;(3)、已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.28.如图,已知点A(﹣1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=90°,抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M.
 (1)、求抛物线y=ax2+bx+c的解析式;(2)、试判断直线CM与以AB为直径的圆的位置关系,并加以证明;(3)、在抛物线上是否存在点N,使得S△BCN=4?如果存在,那么这样的点有几个?如果不存在,请说明理由.
(1)、求抛物线y=ax2+bx+c的解析式;(2)、试判断直线CM与以AB为直径的圆的位置关系,并加以证明;(3)、在抛物线上是否存在点N,使得S△BCN=4?如果存在,那么这样的点有几个?如果不存在,请说明理由.