2011年四川省绵阳市中考数学试卷
试卷更新日期:2017-05-11 类型:中考真卷
一、选择题:
-
1. ﹣1﹣2的结果是( )
A、﹣1 B、﹣3 C、1 D、32. 下列运算正确的是( )A、a+a2=a3 B、2a+3b=5ab C、(a3)2=a9 D、a3÷a2=a3. 抛掷一个质地均匀且六个面上依次刻有1﹣6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是( ) A、出现的点数是7 B、出现的点数不会是0 C、出现的点数是2 D、出现的点数为奇数4. 函数 有意义的自变量x的取值范围是( )A、x≤ B、x≠ C、x≥ D、x<5. 将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( )
A、出现的点数是7 B、出现的点数不会是0 C、出现的点数是2 D、出现的点数为奇数4. 函数 有意义的自变量x的取值范围是( )A、x≤ B、x≠ C、x≥ D、x<5. 将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( )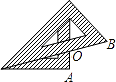 A、75° B、95° C、105° D、120°6. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )
A、75° B、95° C、105° D、120°6. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ) A、0根 B、1根 C、2根 D、3根7. 下列关于矩形的说法,正确的是( )A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分8. 由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )
A、0根 B、1根 C、2根 D、3根7. 下列关于矩形的说法,正确的是( )A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分8. 由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )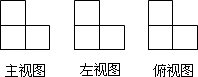 A、
A、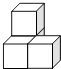 B、
B、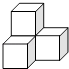 C、
C、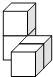 D、
D、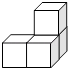 9. 灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15包.请问这次采购派男女村民各多少人?( )A、男村民3人,女村民12人 B、男村民5人,女村民10人 C、男村民6人,女村民9人 D、男村民7人,女村民8人10. 周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的
9. 灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15包.请问这次采购派男女村民各多少人?( )A、男村民3人,女村民12人 B、男村民5人,女村民10人 C、男村民6人,女村民9人 D、男村民7人,女村民8人10. 周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ≈1.414, ≈1.732)( )
 A、36.21米 B、37.71米 C、40.98米 D、42.48米11. 已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )
A、36.21米 B、37.71米 C、40.98米 D、42.48米11. 已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )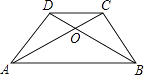 A、 cm2 B、 cm2 C、 cm2 D、 cm212. 若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )
A、 cm2 B、 cm2 C、 cm2 D、 cm212. 若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )
A、x1<x2<a<b B、x1<a<x2<b C、x1<a<b<x2 D、a<x1<b<x2二、填空题:
-
13. 分解因式:a3﹣a= .
14. 如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A=度.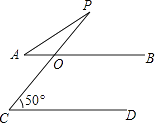 15. 2011年4月第六次全国人口普查,结果显示:绵阳市常住人口为461万人,用科学记数法表示这一数据为 .16. 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为 .
15. 2011年4月第六次全国人口普查,结果显示:绵阳市常住人口为461万人,用科学记数法表示这一数据为 .16. 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为 . 17. 如图,将长8厘米,宽4厘米的矩形纸片ABCD折叠,使A与C重合,则折痕EF的长等于cm.
17. 如图,将长8厘米,宽4厘米的矩形纸片ABCD折叠,使A与C重合,则折痕EF的长等于cm. 18.
18.观察下面的图形,它们是按一定规律排列的,依照此规律,第个图形共有 120个★.

三、解答题
-
19.(1)、化简: ;(2)、解方程: .20. 鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查.

通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
(1)、请你补全下面的数据统计表:家装风格统计表
装修风格
划记
户数
百分比
A中式
正正正正正
25
50%
B欧式
C韩式
5
10%
D其他
正
10%
合计
50
100%
(2)、请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)(3)、如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?21. 右图中曲线是反比例函数 的图象的一支. (1)、这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?(2)、若一次函数 的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.22. 如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆O与BC相切.
(1)、这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?(2)、若一次函数 的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.22. 如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆O与BC相切. (1)、求证:OB⊥OC;(2)、若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积.23. 王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)、请用a表示第三条边长;(2)、问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;(3)、能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.24. 已知抛物线y=x2﹣2x+m﹣1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)、求证:OB⊥OC;(2)、若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积.23. 王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)、请用a表示第三条边长;(2)、问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;(3)、能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.24. 已知抛物线y=x2﹣2x+m﹣1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.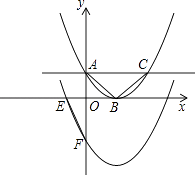 (1)、求m的值;(2)、过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(1)、求m的值;(2)、过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;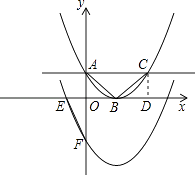 (3)、将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.25. 已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图.
(3)、将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.25. 已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图.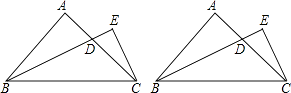 (1)、若BD是AC的中线,求 的值;(2)、若BD是∠ABC的角平分线,求 的值;(3)、结合(1)、(2),试推断 的取值范围(直接写出结论,不必证明),并探究 的值能小于 吗?若能,求出满足条件的D点的位置;若不能,说明理由.
(1)、若BD是AC的中线,求 的值;(2)、若BD是∠ABC的角平分线,求 的值;(3)、结合(1)、(2),试推断 的取值范围(直接写出结论,不必证明),并探究 的值能小于 吗?若能,求出满足条件的D点的位置;若不能,说明理由.