广东省湛江市徐闻县2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-04-19 类型：期末考试

进入 出卷网 下载

一、选择题（共30分）

  • 1. 如图图形中，既是轴对称图形又是中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 把抛物线y＝﹣x2先向左平移1个单位，再向下平移2个单位，得到的抛物线的表达式是（   ）
    A、y＝﹣（x+1）2+2 B、y＝﹣（x+1）2﹣2 C、y＝（x+1）2+2 D、y＝（x+1）2﹣2

    查看试题解析

  • 3. 如图，在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片，则弓形弦AB的长为（   ）

    A、10cm B、16cm C、24cm D、26cm

    查看试题解析

  • 4. 如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（   ）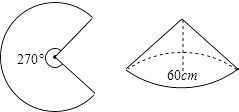

    A、40cm B、50cm C、60cm D、80cm

    查看试题解析

  • 5. 用配方法解方程x2﹣8x+5＝0，将其化为（x+a）2＝b的形式，正确的是（   ）
    A、（x+4）2＝11 B、（x+4）2＝21 C、（x﹣8）2＝11 D、（x﹣4）2＝11

    查看试题解析

  • 6. 点A（﹣3，2）与点B（﹣3，﹣2）的关系是（   ）
    A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、以上各项都不对

    查看试题解析

  • 7. 如图，在△ABC中，AC＝BC＝4，∠ACB＝90°，若点D是AB的中点，分别以点A，B为圆心， 12  AB长为半径画弧，交AC于点E，交BC于点F，则图中阴影部分的面积是（   ）

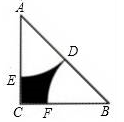    A、16﹣2π B、16﹣π C、8﹣2π D、8﹣π

    查看试题解析

  • 8. 下列事件中，必然事件是（   ）
    A、掷一枚硬币，正面朝上  B、任意三条线段可以组成一个三角形 C、投掷一枚质地均匀的骰子，掷得的点数是奇数   D、抛出的篮球会下落

    查看试题解析

  • 9. 若关于x的一元二次方程x2+x﹣m＝0有实数根，则m的取值范围是（   ）
    A、m≥ 14 B、m≥﹣ 14 C、m≤ 14 D、m≤﹣ 14

    查看试题解析

  • 10. 二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①a＜0，②b＞0，③b2﹣4ac＞0，④a+b+c＜0，其中结论正确的个数有（ ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（共24分）

  • 11. 方程（x﹣1）（x+2）=0的解是 ．

    查看试题解析

  • 12. 如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D．若∠A′DC＝90°，则∠A＝ ．

    查看试题解析

  • 13. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 23 ，则n= ．

    查看试题解析

  • 14. 已知点A（4，y1），B（ 2 ，y2），C（﹣2，y3）都在二次函数y=（x﹣2）2﹣1的图象上，则y1、y2、y3的大小关系是 ．

    查看试题解析

  • 15. 如图，PA，PB分别与⊙O相切于A、B两点，点C为劣弧AB上任意一点，过点C的切线分别交AP，BP于D，E两点．若AP＝8，则△PDE的周长为 ．

    查看试题解析

三、解答题（一）（共18分）

  • 16. 解方程：3x2﹣6x+1＝2．

    查看试题解析

  • 17.
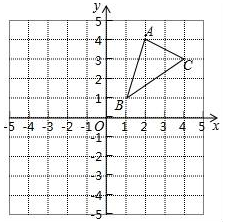    (1)、请画出△ABC关于x轴对称的△A1B1C1 ， 并写出点A1的坐标．
    (2)、请画出△ABC绕点B逆时针旋转90°后的△A2BC2 ．
    (3)、求出（2）中C点旋转到C2点所经过的路径长（结果保留根号和π）．

    查看试题解析

  • 18. 已知：抛物线y＝ax2+bx+3经过点A（3，0）、B（﹣1，8），求抛物线的函数表达式，并通过配方写出抛物线的顶点坐标．

    查看试题解析

四、解答题（二）（共21分）

  • 19. 2015年底某市汽车拥有量为100万辆，而截止到2017年底，该市的汽车拥有量已达到144万辆．
    (1)、求2015年底至2017年底该市汽车拥有量的年平均增长率；
    (2)、若年增长率保持不变，预计2018年底该市汽车拥有量将达到多少万辆．

    查看试题解析

  • 20. 某校在宣传“民族团结”活动中，采用四种宣传形式：A．器乐，B．舞蹈，C．朗诵，D．唱歌．每名学生从中选择并且只能选择一种最喜欢的，学校就宣传形式对学生进行了抽样调查，并将调查结果绘制了如下两幅不完整的统计图．

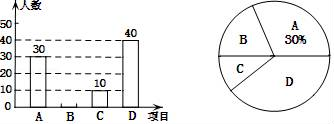
    请结合图中所给信息，解答下列问题：

    (1)、本次调查的学生共有人；
    (2)、补全条形统计图；
    (3)、该校共有1200名学生，请估计选择“唱歌”的学生有多少人？
    (4)、七年一班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位同学表现优秀，现从这四位同学中随机选出两名同学参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．

    查看试题解析

  • 21. 如图，AD是△ABC外角∠EAC的平分线，AD与△ABC的外接圆⊙O交于点D．

    (1)、求证：DB＝DC；
    (2)、若∠CAB＝30°，BC＝4，求劣弧 CD⌢ 的长度．

    查看试题解析

五、解答题（三）（共27分）

  • 22. 某种新商品每件进价是120元，在试销期间发现，当每件商品售价为130元时，每天可销售70件，当每件商品售价高于130元时，每涨价1元，日销售量就减少1件．据此规律，请回答：
    (1)、当每件商品售价定为170元时，每天可销售多少件商品商场获得的日盈利是多少？
    (2)、在商品销售正常的情况下，每件商品的涨价为多少元时，商场日盈利最大？最大利润是多少？

    查看试题解析

  • 23. 如图，在△ABC中，∠C＝90°，∠ABC的平分线BE交AC于点E，过点E作直线BE的垂线交AB于点F，⊙O是△BEF的外接圆．

    (1)、求证：AC是⊙O的切线；
    (2)、过点E作EH⊥AB于点H，求证：EF平分∠AEH；
    (3)、求证：CD＝HF．

    查看试题解析

  • 24. 如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．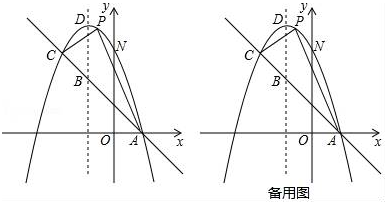

    (1)、求抛物线及直线AC的函数关系式；
    (2)、若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；
    (3)、在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．

    查看试题解析