广东省汕头市潮南区司马浦镇2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期：2019-04-19 类型：期末考试
一、选择题（共30分）
-
1. 已知⊙O中最长的弦为8cm，则⊙O的半径为（ ）cm．A、2 B、4 C、8 D、162. 下列事件属于随机事件的是（ ）A、抛出的篮球会下落 B、两枚骰子向上一面的点数之和大于1 C、买彩票中奖 D、口袋中只装有10个白球，从中摸出一个黑球3. 在下列这些汽车标识中，是中心对称图形的是（ ）A、
B、
C、
D、
4. 抛物线y＝x2+2的图象与y轴的交点坐标是（ ）A、（﹣2，0） B、（2，0） C、（0，﹣2） D、（0，2）5. 如图，在⊙O中，弦AB与CD交于点E，BE＝DE，∠B＝40°，则∠A的度数是（ ）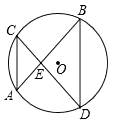
A、20° B、30° C、40° D、80°6. 在“弘扬传统美德传承红色基因”这句话中任选一个字这个字是“传”的概率为（ ）A、 B、 C、 D、7. 关于x的方程kx2+2x﹣1＝0有两个实数根，则k的取值范围是（ ）A、k≥1 B、k≥﹣1 C、k≥1且k≠0 D、k≥﹣1且k≠08. 如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（ ）
A、∠ABD＝∠E B、∠CBE＝∠C C、AD∥BC D、AD＝BC9. 一个等腰三角形的底边长是5，腰长是一元二次方程x2﹣6x+8＝0的一个根，则此三角形的周长是（ ）A、12 B、13 C、14 D、12或1410. 如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；、②3a+c＞0；③当x＞0时，y随x的增大而减小；④当y＞0时，x的取值范围是﹣1＜x＜3；⑤方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；其中结论正确的个数是（ ）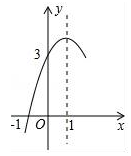
A、4个 B、3个 C、2个 D、1个二、填空题（共24分）
-
11. 方程x2＝3的解是 ．12. 函数y＝x2+bx﹣c的图象经过点（2，4），则2b﹣c的值为 ．13. 分别从数﹣3，﹣2，1，5中，任取两个不同的数，则所取两数的和为正数的概率为 ．14. ⊙O的直径为20，弦AB长为12，点P是弦AB上一点，则OP的取值范围是 ．15. 如图，将矩形ABCD绕点A旋转至矩形AB'C'D'位置，此时AC'的中点恰好与D点重合，AB'交CD于点E．若DE＝1，则AC的长为 ．
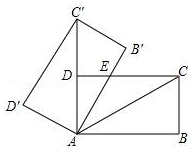16. 定义运算“*”，规定x*y＝ax2+by，其中a、b为常数，且1*2＝5，2*1＝6，则3*8＝ ．三、解答题（一）（共18分）
-
17. 解方程：2（x﹣3）＝3x（3﹣x）18. 汕头有丰富的旅游资源、小陈利用假日来汕头游玩，上午从A、B、C三个景点中任意选择一个游玩，下午从D、E两个景点中任意选择一个游玩，用列表或画树状图的方法列出所有等可能的结果，并求小陈恰好选中景点B和E的概率．19. 如图在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得△AB1C1 ， 使点C1落在直线BC上（点C1与点C不重合），求证：AB1∥CB．
四、解答题（二）（共21分）
-
20. 如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣4，4），B（﹣2，5），C（﹣2，1）．
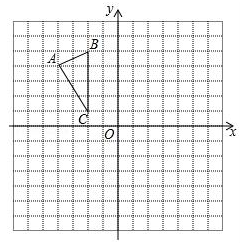(1)、将△ABC绕点（0，3）旋转180°，得到△A1B1C1 ， 画出旋转后的△A1B1C1；(2)、求（1）中的点C旋转到点C1时，点C经过的路径长（结果保留π）．21. 已知：关于x的一元二次方程kx2﹣（4k+1）x+3k+3＝0（k是整数）．(1)、求证：方程有两个不相等的实数根；(2)、若方程的两个实数根都是整数，求k的值．22. 如图，在四边形ABCD中，AD＝BC，∠B＝∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE．
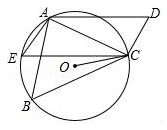(1)、求证：四边形AECD为平行四边形；(2)、连接CO，求证：CO平分∠BCE．五、解答题（三）（共27分）
-
23. 如图，△BCD内接于⊙O，直径AB经过弦CD的中点M，AE交BC的延长线于点E，连接AC，∠EAC＝∠ABD＝30°．
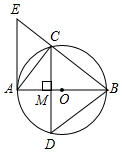(1)、求证：△BCD是等边三角形；(2)、求证：AE是⊙O的切线；(3)、若CE＝2，求⊙O的半径．24. 为响应荆州市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB＝xm，面积为ym2（如图）．
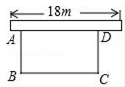(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；(2)、若矩形空地的面积为160m2 ， 求x的值；(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．甲
乙
丙
单价（元/棵）
14
16
28
合理用地（m2/棵）
0.4
1
0.4
25. 在平面直角坐标系xOy中（如图）．已知抛物线y＝﹣ x2+bx+c经过点A（﹣1，0）和点B（0， ），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．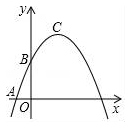
(1)、求这条抛物线的表达式；(2)、求线段CD的长；(3)、将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．