广东省深圳市2018-2019学年八年级数学下学期 第三章图形的平移与旋转 单元卷
试卷更新日期:2019-04-19 类型:单元试卷
一、选择题。(共36分)
-
1. 如图,哪一个选项的右边图形可由左边图形平移得到( )A、
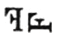 B、
B、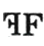 C、
C、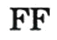 D、
D、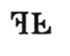 2. 下列所给图形既是中心对称图形又是轴对称图形的是( )A、
2. 下列所给图形既是中心对称图形又是轴对称图形的是( )A、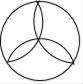 B、
B、 C、
C、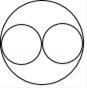 D、
D、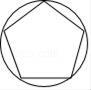 3. 下列运动属于平移的是( )A、急刹车时汽车在地面上的滑动 B、投篮时的篮球运动 C、冷水加热过程中小气泡上升成为大气泡 D、随风飘动的树叶在空中的运动4. 如图,把△ABC沿直线BC方向平移到△DEF,则下列结论错误的是( )
3. 下列运动属于平移的是( )A、急刹车时汽车在地面上的滑动 B、投篮时的篮球运动 C、冷水加热过程中小气泡上升成为大气泡 D、随风飘动的树叶在空中的运动4. 如图,把△ABC沿直线BC方向平移到△DEF,则下列结论错误的是( )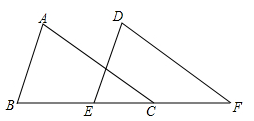 A、∠A=∠D B、BE=CF C、AC=DE D、AB∥DE5. 下列图形中,绕某个点旋转180°能与自身重合的图形有( )
A、∠A=∠D B、BE=CF C、AC=DE D、AB∥DE5. 下列图形中,绕某个点旋转180°能与自身重合的图形有( )①正方形;②等边三角形;③长方形;④角;⑤平行四边形;⑥圆
A、2个 B、3个 C、4个 D、5个6. 如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'O'B',若∠AOB=15°,则∠AOB'的度数是( )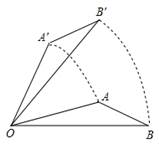 A、25° B、30° C、35° D、40°7. 北京时间9时整,钟面上的时针和分针的夹角是( )度.A、30 B、45 C、60 D、908. 在平面直角坐标系中,点M(-1,3),先向右平移2个单位,再向下平移4个单位,得到的点的坐标为( )A、(-3,-1) B、(-3,7) C、(1,-1) D、(1,7)9. 如图,矩形ABCD的对角线AC=5,BC=4,则图中五个小矩形的周长之和为( )
A、25° B、30° C、35° D、40°7. 北京时间9时整,钟面上的时针和分针的夹角是( )度.A、30 B、45 C、60 D、908. 在平面直角坐标系中,点M(-1,3),先向右平移2个单位,再向下平移4个单位,得到的点的坐标为( )A、(-3,-1) B、(-3,7) C、(1,-1) D、(1,7)9. 如图,矩形ABCD的对角线AC=5,BC=4,则图中五个小矩形的周长之和为( )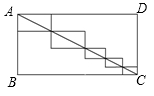 A、7 B、9 C、14 D、1810. 如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标是( )
A、7 B、9 C、14 D、1810. 如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标是( )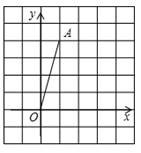 A、(1,4) B、(4,1) C、(4,-1) D、(2,3)11. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图所示看到的万花简的一个图案,如图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是把四边形ABCD以A为旋转中心( )
A、(1,4) B、(4,1) C、(4,-1) D、(2,3)11. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图所示看到的万花简的一个图案,如图中所有小三角形均是全等的等边三角形,其中的四边形AEFG可以看成是把四边形ABCD以A为旋转中心( )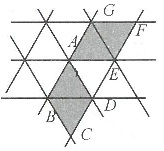 A、顺时针旋转60°得到 B、逆时针旋转60°得到 C、顺时针旋转120°得到 D、逆时针旋转120°得到12. 如图①中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图①作为“基本图形”绕着A点经过逆时针旋转得到图②.两次旋转的角度分别为( )
A、顺时针旋转60°得到 B、逆时针旋转60°得到 C、顺时针旋转120°得到 D、逆时针旋转120°得到12. 如图①中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图①作为“基本图形”绕着A点经过逆时针旋转得到图②.两次旋转的角度分别为( )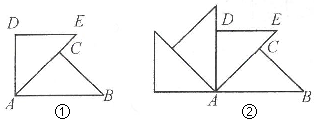 A、45°,90° B、90°,45° C、60°,30° D、30°,60°
A、45°,90° B、90°,45° C、60°,30° D、30°,60°二、填空题。(共12分)
-
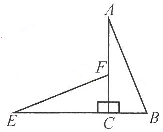
13. 如图,在平面内将Rt△ABC绕直角顶点C逆时针旋转90°得到Rt△EFC.若AB= ,BC=1,则线段BE的长为.
 14. 如图,在平面内将△ABC绕点B旋转至△A'BC'的位置时,有AC//BC',∠C=40°,则旋转的角度是.
14. 如图,在平面内将△ABC绕点B旋转至△A'BC'的位置时,有AC//BC',∠C=40°,则旋转的角度是.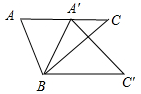 15. 如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任作一条直线分别交AD,BC于E,F,则阴影部分的面积是
15. 如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任作一条直线分别交AD,BC于E,F,则阴影部分的面积是 16. 如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为.
16. 如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为.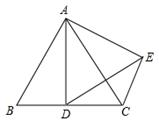
三、解答题。(共52分)
-
17. 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
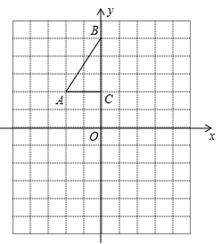 (1)、将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形;(2)、平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形;(3)、若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.18. 如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F.
(1)、将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形;(2)、平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形;(3)、若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.18. 如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC交AB于点F.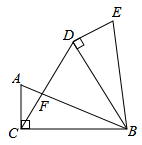 (1)、求∠ABE的度数;(2)、求DC的长;(3)、求△ACF与△BDF的周长之和是多少?19. 阅读下面材料.
(1)、求∠ABE的度数;(2)、求DC的长;(3)、求△ACF与△BDF的周长之和是多少?19. 阅读下面材料.如图①,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;
如图②,以BC为轴,把△ABC翻折180°,可以变到△DBC的位置;
如图③,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
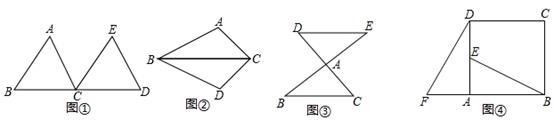
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
(1)、在图④中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF的位置;(2)、指出图中线段BE与DF之间数量和位置关系,并详明理由.20.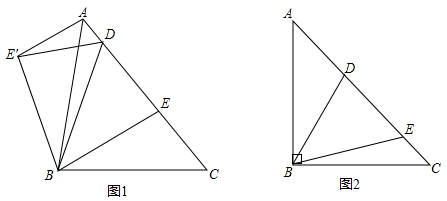 (1)、如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE< ∠ABC).以点B为旋转中心,将△BEC按逆时针旋转∠ABC,得到△BE'A(点C与点A重合,点E到点E’处)连接DE',求证:DE'=DE;(2)、如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE<45°).求证:DE2=AD2+EC2.
(1)、如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE< ∠ABC).以点B为旋转中心,将△BEC按逆时针旋转∠ABC,得到△BE'A(点C与点A重合,点E到点E’处)连接DE',求证:DE'=DE;(2)、如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE<45°).求证:DE2=AD2+EC2.