广东省深圳市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-04-19 类型：期末考试

进入出卷网下载

一、选择题（共36分）

1. 下列实数中，最大的是（）

A、-2 B、0 C、 $\frac{1}{4}$ D、 $\sqrt{2}$

查看试题解析
2. 下列各组数中不能作为直角三角形三边长的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、7，24，25 C、4，5，6 D、 $\frac{3}{5}$ ， $\frac{4}{5}$ ，1

查看试题解析
3. 直线a、b、c、d的位置如图，如果∠1=115°，∠2=115°，∠3=124°，那么∠4等于（）

A、56° B、60° C、65° D、66°

查看试题解析
4. 下列根式中是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{8}$ C、 $\sqrt{10}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
5. 已知点M向左平移3个单位长度后的坐标为（-1，2），则点M原来的坐标为（）

A、（-4，2） B、（2，2） C、（-1，3） D、（-1，-2）

查看试题解析
6. 在一次艺术作品制作比赛中，某小组八件作品的成绩（单位：分）分别是：7、9、8、9、8、10、9、7，下列说法不正确的是（）

A、中位数是8.5 B、平均数是8.4 C、众数是9 D、极差是3

查看试题解析
7. 以方程组 ${\begin{matrix} y = 2 x - 4 \\ 3 x + y = 1 \end{matrix}$ 的解为坐标的点（a，b）在平面直角坐标系的（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 下列命题是假命题的是（）

A、49的平方根是±7 B、点M（1，a）和点N（3，b）是一次函数y=-2x+1图象上的两点，则a>b C、无限小数都是无理数 D、点（-2，3）到y轴的距离是2

查看试题解析
9. 一次函数=kx-k（k<0）的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 小明从A地前往B地，到达后立刻返回，他与A地的距离y（千米）和所用时间x（小时）之间的函数关系如图所示，则小明出发6小时后距A地（）

A、120千米 B、160千米 C、180千米 D、200千米

查看试题解析
11. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五，屈绳量之，不足一尺，问木长几何？”大致意思是：“用一根绳子去量一根木条，绳子剩余4.5尺，将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”，设绳子长x尺，木条长y尺，根据题意所列方程组正确的是（）

A、 ${\begin{matrix} x - y = 4.5 \\ \frac{1}{2} x - y = 1 \end{matrix}$ B、 ${\begin{matrix} x - y = 4.5 \\ y - \frac{1}{2} x = 1 \end{matrix}$ C、 ${\begin{matrix} x + y = 4.5 \\ y - \frac{1}{2} x = 1 \end{matrix}$ D、 ${\begin{matrix} x - y = 4.5 \\ x - \frac{1}{2} y = 1 \end{matrix}$

查看试题解析
12. 如图，在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，点D从点A出发以每秒1cm的速度向点C运动，当点D运动到线段AB的中垂线与线段AC的交点处时，运动时间是（）

A、 $\frac{25}{2}$ 秒 B、 $\frac{25}{4}$ 秒 C、 $\frac{13}{2}$ 秒 D、 $\frac{7}{2}$ 秒

查看试题解析

二、填空题（共12分）

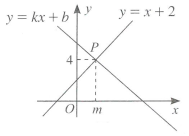
13. 若点M（a-3，a+1）在y轴上，则点M的坐标为.

查看试题解析
14. 如图，一次函数y=x+2与y=kx+b的图象相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是.

查看试题解析
15. 已知一组数据为：5，3，3，6，3，则这组数据的方差是．

查看试题解析
16. 如图，在平面直角坐标系中，点A（12，0），点B（0，4），点P是直线y=-x-1上一点，且∠ABP=45°，则点P的坐标为.

查看试题解析

三、解答题（共52分）

17. 计算：

(1)、 $\sqrt{18} - \sqrt{8} + \sqrt[3]{- 8}$

(2)、 $(\sqrt{12} + 2 \sqrt{6}) \times \sqrt{3} - 12 \sqrt{\frac{1}{2}}$

查看试题解析
18. 解方程组： ${\begin{matrix} 2 x - 3 y = 5 \\ 3 x + y = 2 \end{matrix}$

查看试题解析
19. 4月23日是世界读书日，某校开展了“书香校园”主题教育活动，鼓励师生利用课余时间）广泛阅读。本学期末，学校为了调查这学期学生课外阅读情况，学校学生会随机抽样调查了一部分学生阅读课外书的本数，并将收集到的数据整理成如图的统计图.

(1)、这次一共调查的学生人数是人；

(2)、所调查学生读书本数的众数是本，中位数是本；

(3)、若该校有800名学生，请你估计该校学生这学期读书总数是多少本？

查看试题解析
20. 如图，已知点E在线段AD上，点P在直线CD上，∠AEF=∠F，∠BAD=∠CPF.
求证：∠ABD+∠BDC=180°.

查看试题解析
21. 某一天，水果经营户老张用1600元从水果批发市场购进猕猴桃和芒果共50千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：

品名

猕猴桃

芒果

批发价（元/千克）

20

40

零售价（元/千克）

26

50

(1)、他购进猕猴桃和芒果各多少千克？

(2)、如果猕猴桃和芒果全部卖完，他能赚多少钱？

查看试题解析
22. 如图所示，在平面直角坐标系中，已知A（0，1）、B（2，0）、C（4，3）.

(1)、在平面直角坐标系中画出△ABC，则此△ABC的面积是 ▲ ；

(2)、若点D与点C关于y轴对称，则点D的坐标为；

(3)、已知P为x轴上一点，若△ABP的面积为4，求点P的坐标.

查看试题解析
23. 如图1，在平面直角坐标系中将直线y=2x+1向下平移3个单位长度得到直线 $l_{1}$ ，直线 $l_{1}$ 与x轴交于点C.直线 $l_{2}$ ：y=x+2与x轴、y轴分别交于A、B两点，且与直线 $l_{1}$ 交于点D.

(1)、填空：点A的坐标为，点B的坐标为；

(2)、直线 $l_{1}$ 的函数表达式为；

(3)、在直线 $l_{1}$ 上是否存在点E，使S_△AOE=2S△_ABO？若存在，则求出点E的坐标；若不存在，请说明理由；

(4)、如图2，点P为线段AD上一点（不含端点），连接CP，一动点H从点C出发，沿线段CP以每秒1个单位的速度运动到点P，再沿线段PD以每秒 $\sqrt{2}$ 个单位的速度运动到点D后停止，求点H在整个运动过程中所用时间最少时点P的坐标.

查看试题解析

品名	猕猴桃	芒果
批发价（元/千克）	20	40
零售价（元/千克）	26	50