浙江省温州市苍南县六校2018-2019学年九年级下学期数学中考一模联考试卷
试卷更新日期:2019-04-19 类型:中考模拟
一、选择题(本题有10个小题,每小题4分,共40分,)
-
1. 2的相反数为( )A、 -2 B、2 C、 D、2. 为缓解中低收入人群和新参加工作的大学生住房的需求,某市将新建保障住房4800000平方米,把4800000用科学记数法表示应是( )A、0.48×107 B、4.8×106 C、4.8×107 D、48×1053. 从甲,乙,丙三人中任选一名代表,甲被选中的可能性是( )A、 B、1 C、 D、4. 与如图所示的三视图对应的几何体是( )
 A、
A、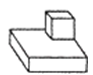 B、
B、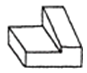 C、
C、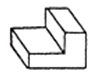 D、
D、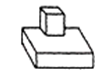 5. 不等式-2x+1<0的解集是( )A、x> B、x> C、x< D、x<6. 一次函数y1=x+1与y2=-2x+4图像交点的横坐标是( )A、4 B、2 C、1 D、07. “五一”前夕,某校社团进行爱心义卖活动,先用800元购进第一批康乃馨,包装后售完,接着又用400元购进第二批康乃馨,已知第二批所购数量是第一批所购数量的 ,且康乃馨的单价比第一批的单价多1元,设第一批康乃馨的单价是x元,则下列方程正确的是( )A、 +1= B、 = C、 × = D、800x=3×400(x+1)8. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则 的长( )
5. 不等式-2x+1<0的解集是( )A、x> B、x> C、x< D、x<6. 一次函数y1=x+1与y2=-2x+4图像交点的横坐标是( )A、4 B、2 C、1 D、07. “五一”前夕,某校社团进行爱心义卖活动,先用800元购进第一批康乃馨,包装后售完,接着又用400元购进第二批康乃馨,已知第二批所购数量是第一批所购数量的 ,且康乃馨的单价比第一批的单价多1元,设第一批康乃馨的单价是x元,则下列方程正确的是( )A、 +1= B、 = C、 × = D、800x=3×400(x+1)8. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则 的长( )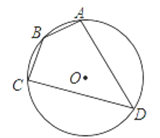 A、 B、 C、 D、9. 如图,正方形ABCD中,内部有4个全等的正方形,小正方形的顶点E,F,G,H分别在边AB,BC,CD,AD上,则tan∠AEH=( )
A、 B、 C、 D、9. 如图,正方形ABCD中,内部有4个全等的正方形,小正方形的顶点E,F,G,H分别在边AB,BC,CD,AD上,则tan∠AEH=( )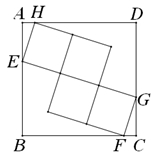 A、 B、 C、 D、10. 如图,⊙O的半径为2 ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为( )
A、 B、 C、 D、10. 如图,⊙O的半径为2 ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为( )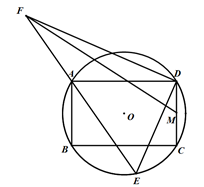 A、 B、6+ C、 D、
A、 B、6+ C、 D、二、 填空题(本题共6个小题,每小题5分,共30分)
-
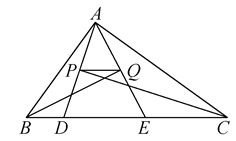
11. 分解因式: = .12. 已知 ,则 .13. 今年3月份某周,我市每天的最高气温(单位:℃)12,11,10,15,16,15,12,若这组数据的中位数是.14. 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为.
 15. 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点B的坐标为(12,6),反比例函数 的图象分别交边BC、AB于点D、E,连结DE,ΔDEF与ΔDEB关于直线DE对称.当点F正好落在边OA上时,则k的值为 .
15. 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点B的坐标为(12,6),反比例函数 的图象分别交边BC、AB于点D、E,连结DE,ΔDEF与ΔDEB关于直线DE对称.当点F正好落在边OA上时,则k的值为 .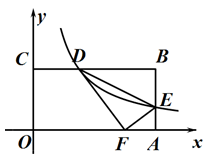 16. 自行车车轮的辐条编制方式是多种多样的,同样大小的车轮,辐条编法不同,辐条的长度是不一样的,图2和图3是某种“24吋(指轮圈直径)”车轮一侧的辐条编法示意图,两个同心圆分别代表轮圈和花鼓,连接两圆的线段代表辐条,轮圈和花鼓上的穿辐条的孔都等分圆周,图2是直拉式编法,每根辐条的延长线都过圆心,优点是编法简单,缺点是轮强度较低,且力传递的效果较差,所以一般都采用如图3(两图中孔的位置一样)这样的错位式编法,若弧DC的长度和弧AB相等,则BE的长度为吋.
16. 自行车车轮的辐条编制方式是多种多样的,同样大小的车轮,辐条编法不同,辐条的长度是不一样的,图2和图3是某种“24吋(指轮圈直径)”车轮一侧的辐条编法示意图,两个同心圆分别代表轮圈和花鼓,连接两圆的线段代表辐条,轮圈和花鼓上的穿辐条的孔都等分圆周,图2是直拉式编法,每根辐条的延长线都过圆心,优点是编法简单,缺点是轮强度较低,且力传递的效果较差,所以一般都采用如图3(两图中孔的位置一样)这样的错位式编法,若弧DC的长度和弧AB相等,则BE的长度为吋.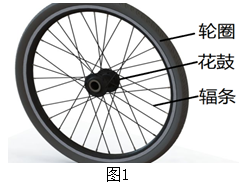
三、解答题(本题共8个小题,共80分)
-
17.(1)、计算:3sin30°+(2)、化简:18. 某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
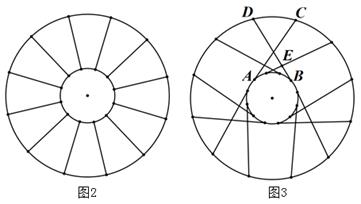
 (1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?.19. 如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.
(1)、求本次被调查的学生人数;(2)、补全条形统计图;(3)、该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?.19. 如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高. (1)、求证:四边形ADEF是平行四边形;(2)、若∠AHF=20°,∠AHD=50°,求∠DEF的度数.20. 如图,网格中有一条线段AB,点A、B都在格点上,网格中的每个小正方形的边长为1.
(1)、求证:四边形ADEF是平行四边形;(2)、若∠AHF=20°,∠AHD=50°,求∠DEF的度数.20. 如图,网格中有一条线段AB,点A、B都在格点上,网格中的每个小正方形的边长为1. (1)、在图①中画出格点△ABC,使△ABC是等腰三角形;(2)、以AB为斜边作Rt△ABC(见图②),在图②中找出格点D,作锐角△ADC,且使得∠ADC=∠B.21. 如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,∠P=30°.
(1)、在图①中画出格点△ABC,使△ABC是等腰三角形;(2)、以AB为斜边作Rt△ABC(见图②),在图②中找出格点D,作锐角△ADC,且使得∠ADC=∠B.21. 如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,∠P=30°.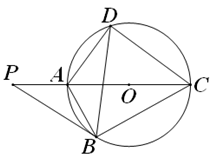 (1)、求证:PB=BC;
(1)、求证:PB=BC;
(2)、若AD=6,tan∠DCA= ,求BD的长.
22. 已知如图,抛物线 交x轴于A、C两点,点D是x轴上方抛物线上的点,以A,D为顶点按逆时针方向作正方形ADEF.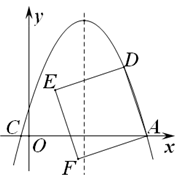
 (1)、求点A的坐标和抛物线的对称轴的表达式;(2)、当点F落在对称轴上时,求出点D的坐标;
(1)、求点A的坐标和抛物线的对称轴的表达式;(2)、当点F落在对称轴上时,求出点D的坐标;
(3)、连接OD交EF于点G,记OA和EF交于点H,当△AFH的面积是四边形ADEH面积的 时,则 =.(直接写出答案)
23. 一连锁店销售某品牌商品,该商品的进价是60元.因为是新店开业,所以连锁店决定当月前10天进行试营业活动,活动期间该商品的售价为每件80元,据调查研究发现:当天销售件数 (件)和时间第x(天)的关系式为 ( ),已知第4天销售件数是40件,第6天销售件数是44件.活动结束后,连锁店重新制定该商品的销售价格为每件100元,每天销售的件数也发生变化:当天销售数量 (件)与时间第x(天)的关系为: ( ).(1)、求 关于x的函数关系式;
(2)、若某天的日毛利润是1120元,求x的值;(3)、因为该连锁店是新店开业,所以试营业结束后,厂家给这个连锁店相应的优惠政策:当这个连锁店日销售量达到60件后(不含60),每多销售1件产品,当日销售的所有商品进价减少2元,设该店日销售量超过60件的毛利润总额为W,请直接写出W关于x的函数解析式,及自变量x的取值范围: .
24. 在矩形ABCD中,AB=6,BC=8,BE⊥AC于点E,点O是线段AC上的一点,以AO为半径作圆O交线段AC于点G,设AO=m.
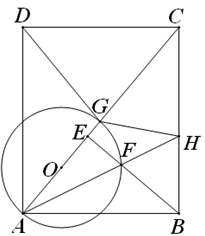 (1)、直接写出AE的长:AE=;
(1)、直接写出AE的长:AE=;
(2)、取BC中点P,连接PE,当圆O与△BPE一边所在的直线相切时,求出m的长;
(3)、设圆O交BE于点F,连接AF并延长交BC于点H.①连接GH,当BF=BH时,求△BFH的面积;
②连接DG,当tan∠HFB=3时,直接写出DG的长,DG .