湖北省恩施巴东县2018-2019学年九年级下学期数学3月月考试卷

试卷更新日期：2019-04-19 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12个小题，每小题3分，共36分。在每小题给出的四个选项中，恰有一项是符合要求的。）

1. $- \frac{1}{3}$ 的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 鄂州市凤凰大桥，坐落于鄂州鄂城区洋澜湖上，是洋澜湖上在建的第5座桥，大桥长1100m，宽27m，鄂州有关部门公布了该桥新的设计方案，并计划投资人民币2.3亿元，2015年开工，预计2017年完工．请将2.3亿元用科学记数法表示为（）

A、2.3×10⁸ B、0.23×10⁹ C、23×10⁷ D、2.3×10⁹

查看试题解析
3. 如图，AB∥CD，E为CD上一点，射线EF经过点A，EC=EA．若∠CAE=30°，则∠BAF=（）

A、30° B、40° C、50° D、60°

查看试题解析
4. 把x²y﹣2y²x+y³分解因式正确的是( )

A、y（x²﹣2xy+y²） B、x²y﹣y²（2x﹣y） C、y（x﹣y）² D、y（x+y）²

查看试题解析
5. 下列运算正确的是（）

A、x³•x²=x⁶ B、3a²+2a²=5a² C、a（a﹣1）=a²﹣1 D、（a³）⁴=a⁷

查看试题解析
6.
如图是一个正方体的展开图，把展开图折叠成正方体后，有“弘”字一面的相对面上的字是（）

A、传 B、统 C、文 D、化

查看试题解析
7. 关于x的不等式 ${\begin{matrix} 2 (x - 1) > 4 \\ a - x < 0 \end{matrix}$ 的解集为x＞3，那么a的取值范围为（）

A、a＞3 B、a＜3 C、a≥3 D、a≤3

查看试题解析
8. 某交警在一个路口统计的某时段来往车辆的车速情况如表：

车速（km/h）

48

49

50

51

52

车辆数（辆）

5

4

8

2

1

则上述车速的中位数和众数分别是（）

A、50，8 B、50，50 C、49，50 D、49，8

查看试题解析
9. 如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（）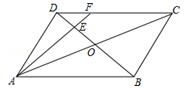

A、1：4 B、1：3 C、2：3 D、1：2

查看试题解析
10. 为配合恩施州市“我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可享受8折优惠．小慧同学到该书店购书，她先买优惠卡再凭卡付款，结果节省了10元．若此次小慧同学不买卡直接购书，则她需付款多少元？（）

A、140元 B、150元 C、160元 D、200元

查看试题解析
11. 如图，已知圆柱的底面直径BC= $\frac{6}{π}$ ，高AB=3，小虫在圆柱表面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为（）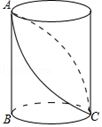

A、 $3 \sqrt{2}$ B、 $3 \sqrt{5}$ C、 $6 \sqrt{5}$ D、 $6 \sqrt{2}$

查看试题解析
12. 二次函数y=ax²+bx+c（a≠0）的图象如图，给出下列四个结论：
①3a+2b+c＜0；②3a+c＜b²-4ac； ③方程2ax²+2bx+2c-5=0没有实数根；④m（am+b）+b＜a（m≠-1）．其中正确结论的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（本大题共有4小题，每小题3分，共12分。不要求写出解答过程，请把答案直接填写在相应的位置上）

13. $\sqrt{25}$ 的平方根是；64的立方根是．

查看试题解析
14. 函数 $y = \frac{\sqrt{3 - x}}{x + 2}$ 的自变量x的取值范围是．

查看试题解析
15. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm， AE=2cm，则OF的长度是．

查看试题解析
16. 把奇数列成下表，根据表中数的排列规律，则上起第8行，左起第6列的数是．

查看试题解析

三、解答题（本大题共有8个小题，共72分。解答时应写出文字说明、证明过程或演算步骤）

17. 先简化，再求值： $\frac{x - 2}{2 x - 6} \div (\frac{- 5}{x - 3} - x - 3)$ ，其中x= $\sqrt{2} - 2$ ．

查看试题解析
18. 如图所示，在梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别为边AB、BC、CD、DA的中点，

求证：四边形EFGH为菱形．

查看试题解析
19. 一个不透明的袋子里装有编号分别为1、2、3的球（除编号以为，其余都相同），其中1号
球1个，3号球3个，从中随机摸出一个球是2号球的概率为 $\frac{1}{3}$ ．

(1)、求袋子里2号球的个数．

(2)、甲、乙两人分别从袋中摸出一个球（不放回），甲摸出球的编号记为x，乙摸出球的编号记为y，
用列表法或画树状图法求点A（x，y）在直线y=x下方的概率．

查看试题解析
20. 如图所示，等边三角形ABC放置在平面直角坐标系中，已知A（0，0）、B（6，0），反比例函数的图象经过点C．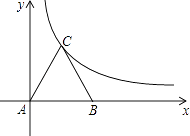

(1)、求点C的坐标及反比例函数的解析式．

(2)、将等边△ABC向上平移n个单位，使点B恰好落在双曲线上，求n的值．

查看试题解析
21. “一炷香”是闻名中外的恩施大峡谷著名的景点．某校综合实践活动小组先在峡谷对面的广场上的A处测得“香顶”N的仰角为45°，此时，他们刚好与“香底”D在同一水平线上．然后沿着坡度为30°的斜坡正对着“一炷香”前行110，到达B处，测得“香顶”N的仰角为60°．根据以上条件求出“一炷香”的高度．（测角器的高度忽略不计，结果精确到1米，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）．

查看试题解析
22. 某商店欲购进甲、乙两种商品，已知甲的进价是乙的进价的一半，进3件甲商品和1件乙商品恰好用200元．甲、乙两种商品的售价每件分别为80元、130元，该商店决定用不少于6710元且不超过6810元购进这两种商品共100件．

(1)、求这两种商品的进价．

(2)、该商店有几种进货方案？哪种进货方案可获得最大利润，最大利润是多少？

查看试题解析
23. 如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．

(1)、求证：CG是⊙O的切线．

(2)、求证：AF=CF．

(3)、若∠EAB=30°，CF=2，求GA的长．

查看试题解析
24. 如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．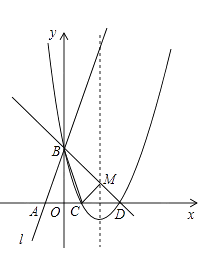

(1)、求直线BD和抛物线的解析式．

(2)、若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．

(3)、在抛物线上是否存在点P，使S_△_PBD=6？若存在，求出点P的坐标；若不存在，说明理由．

查看试题解析

车速（km/h）	48	49	50	51	52
车辆数（辆）	5	4	8	2	1