浙江省桐乡市2019年九年级文理科基础调研数学试卷(3月)
试卷更新日期:2019-04-19 类型:月考试卷
一、选择题(本题有9小题,每小题2分,共18分)
-
1. 下列计算正确的是( )A、(-2)0=0 B、(-2)-1=2 C、6a-5a=1 D、(2a)3=8a32. 要说明命题“若a2>4,则a>2”是假命题,可以举的反例是( )A、a=3 B、a=0 C、a=-3 D、a=-13. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”设鸡x只,兔y只,可列方程组为( )A、 B、 C、 D、4. 用尺规作图法在一个矩形中作菱形ABCD,下列作法正确的是( )A、
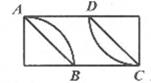 B、
B、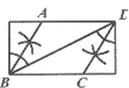 C、
C、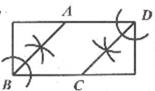 D、
D、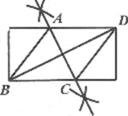 5. 若关于x的不等式2x-m>0的最小整数解为3,则m的取值范围是( )A、4≤m<6 B、4<m<6 C、4≤m≤6 D、4<m≤66. 如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )
5. 若关于x的不等式2x-m>0的最小整数解为3,则m的取值范围是( )A、4≤m<6 B、4<m<6 C、4≤m≤6 D、4<m≤66. 如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )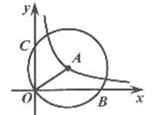 A、2 B、4 C、2 D、67. 如图,正三角形纸片ABC中,D是BC的中点,P是AB边上的一个动点,将△BPD沿PD翻折。得到△QPD.当点P从点A向点B运动时,点Q也随之运动.若AB=6,则点Q经过的路径长是( )
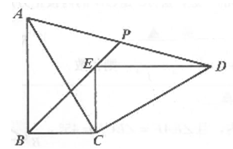
A、2 B、4 C、2 D、67. 如图,正三角形纸片ABC中,D是BC的中点,P是AB边上的一个动点,将△BPD沿PD翻折。得到△QPD.当点P从点A向点B运动时,点Q也随之运动.若AB=6,则点Q经过的路径长是( ) A、3 B、6 C、3π D、6π8. 已知四边形ABCD是任意的凸四边形,E,F,G,H分别是AB,BC,CD,DA的中点,四边形ABCD的周长和面积分别记作C1和S1 , 四边形EFGH的周长和面积分别记作C2和S2 , 设m= ,n= ,则下面说法正确的是( )
A、3 B、6 C、3π D、6π8. 已知四边形ABCD是任意的凸四边形,E,F,G,H分别是AB,BC,CD,DA的中点,四边形ABCD的周长和面积分别记作C1和S1 , 四边形EFGH的周长和面积分别记作C2和S2 , 设m= ,n= ,则下面说法正确的是( )
A、m,n都是定值 B、m是定值,n不是定值 C、m不是定值,n是定值 D、m,n都不是定值9. 如图,直线y=kx+b分别与x轴、,轴的正半轴相交于点A,B,C是OB的中点,D( ,0)在线段OA上.若∠ACD=∠ABO=30°,则b的值为( )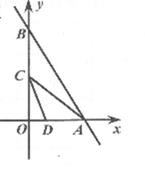 A、6 B、4 C、8 D、10
A、6 B、4 C、8 D、10二、填空题(本题有5小题,每小题3分,共15分)
-
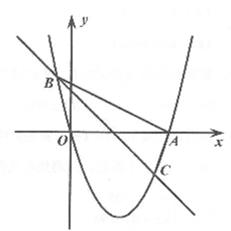
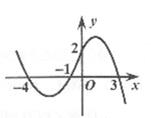
10. 已知,关于x的函数图象如图所示,当y<0时,自变量x的取值范围是 .
 11. 一个布袋内只装有1个红球和2个黄球,这些球除颜色外其余都相同.随机摸出一个球后放回袋内,再随机摸出一个球,则两次摸出的球都是黄球的概率是 .12. 若弦AB是⊙O的内接正十二边形的一边,弦AC是⊙O的内接正方形的一边,弦CB是⊙O的内接正n边形一边,则n的值是 .13. 已知 ,则代数式 的值为 .14. 如图,点E,F在正方形ABCD内,且∠EAF=∠ECF=45°,则线段BE,EF,FD之间的数量关系是 .
11. 一个布袋内只装有1个红球和2个黄球,这些球除颜色外其余都相同.随机摸出一个球后放回袋内,再随机摸出一个球,则两次摸出的球都是黄球的概率是 .12. 若弦AB是⊙O的内接正十二边形的一边,弦AC是⊙O的内接正方形的一边,弦CB是⊙O的内接正n边形一边,则n的值是 .13. 已知 ,则代数式 的值为 .14. 如图,点E,F在正方形ABCD内,且∠EAF=∠ECF=45°,则线段BE,EF,FD之间的数量关系是 .
三、解答题(本题有4小题,共27分)
-
15. 先化简,后求值: ,其中a=1+ ,b=1- .16. 甲、乙两人加工同一种直径为100mm的零件,现从他们加工好的零件中随机各抽取6个,量得零件的直径如下(单位:mm):
甲:98,102,100,100,101,99:
乙:100,103,101,97,100,99.
(1)、根据上述两组数据,完成下面的表格:平均数
中位数
众数
方差
甲
100
乙
100
100
(2)、请你结合(1)中的统计数据,评价一下甲、乙两人的加工质量.