广东省深圳市2018-2019学年七年级下学期数学期中考试模拟卷
试卷更新日期:2019-04-18 类型:期中考试
一、选择题
-
1. 下列计算结果正确的是( )A、a4•a2=a8 B、(a4)2=a6 C、(ab)2=a2b2 D、(a﹣b)2=a2﹣b22. 如果代数式x2+kx+49能分解成(x﹣7)2形式,那么k的值为( )A、7 B、﹣14 C、±7 D、±143. A、B都是五次多项式,则A﹣B一定是( )A、四次多项式 B、五次多项式 C、十次多项式 D、不高于五次的多项式4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线l1∥l2∥l3 , 一等腰直角三角形ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则 的值为( )
 A、 B、 C、 D、6. 如图,已知l1∥l2 , AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )
A、 B、 C、 D、6. 如图,已知l1∥l2 , AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )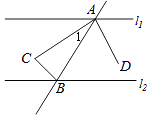 A、1个 B、2个 C、3个 D、4个7. 如图,P是∠AOB平分线上一点,CD⊥OP于P,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
A、1个 B、2个 C、3个 D、4个7. 如图,P是∠AOB平分线上一点,CD⊥OP于P,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.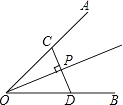 A、小于 B、大于 C、等于 D、不能确定8.
A、小于 B、大于 C、等于 D、不能确定8.如图,不能推出a∥b的条件是( )
 A、∠1=∠3 B、∠1=∠4 C、∠2=∠4 D、∠2+∠3=180°9. 在△ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式中( )A、S,h是变量, , a是常量 B、S,h,a是变量,是常量 C、S,h是变量, , S是常量 D、S是变量, , a,h是常量10. 设半径为r的圆的周长为C,则C=2πr,下列说法错误的是( )A、常量是π和2 B、常量是2 C、用C表示r为r= D、变量是C和r11. 在函数y=中,自变量x的取值范围是( )A、x< B、x≤ C、x> D、x≥12. 2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水x立方米,水费为y元,则y与x的函数关系用图象表示正确的是( )A、
A、∠1=∠3 B、∠1=∠4 C、∠2=∠4 D、∠2+∠3=180°9. 在△ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式中( )A、S,h是变量, , a是常量 B、S,h,a是变量,是常量 C、S,h是变量, , S是常量 D、S是变量, , a,h是常量10. 设半径为r的圆的周长为C,则C=2πr,下列说法错误的是( )A、常量是π和2 B、常量是2 C、用C表示r为r= D、变量是C和r11. 在函数y=中,自变量x的取值范围是( )A、x< B、x≤ C、x> D、x≥12. 2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水x立方米,水费为y元,则y与x的函数关系用图象表示正确的是( )A、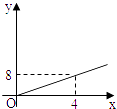 B、
B、 C、
C、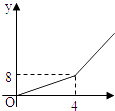 D、
D、
二、填空题
-
13. (2m3)4= .14. 把一张长方形的纸条折叠,如图所示,EF为折痕,若∠EFB=34°,则∠BFD的度数为 .
 15. 把一根长为50cm的铁丝弯成一个长方形,设这个长方形一边的长为xcm,它的面积为ycm2 , 则y与x之间的函数关系式为 , 自变量的取值范围是 .16. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是 .
15. 把一根长为50cm的铁丝弯成一个长方形,设这个长方形一边的长为xcm,它的面积为ycm2 , 则y与x之间的函数关系式为 , 自变量的取值范围是 .16. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是 .
三、解答题
-
17. 计算:(1)、(﹣5x)•(3x2﹣4x+5):(2)、﹣2a•(3ab2﹣5ab3):(3)、(﹣a2b)(2a﹣ab+3b);(4)、﹣2xn•(﹣3xn+1+4xn﹣1).18. 先化简,再求值:当 时,求 .19.
如图AE平分∠BAD,BE平分∠ABC,∠α+∠β=90°,试说明∠C+∠D=180°.
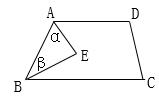 20. 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
20. 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.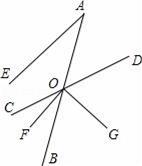 (1)、求∠DOF的度数;(2)、试说明OD平分∠AOG.21. 老师告诉小红:“离地面越高,温度越低”.并给小红出示了下面的表格:
(1)、求∠DOF的度数;(2)、试说明OD平分∠AOG.21. 老师告诉小红:“离地面越高,温度越低”.并给小红出示了下面的表格:距离地面高度/千米
0
1
2
3
4
5
温度/摄氏度
20
14
8
2
-4
-10
根据上表,老师还给小红出了下面几个问题,请你和小红一起来回答
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用h表示距离地面的高度,用t表示温度,请你用关于h的式子表示t;(3)、请你利用(2)的结论求①距离地面5千米的高空温度是多少?
②当高空某处温度为﹣40度时,求该处的高度.

