2011年广西南宁市中考数学试卷
试卷更新日期:2017-05-10 类型:中考真卷
一、选择题
-
1. 下列所给的数中,是2的相反数的是( )A、﹣2 B、 C、2 D、﹣2.
如图,三视图描述的实物形状是( )
 A、棱柱 B、棱锥 C、圆柱 D、圆锥3. 下列各式计算正确的是( )A、10a6÷5a2=2a4 B、3 +2 =5 C、2(a2)3=6a6 D、(a﹣2)2=a2﹣44. 我国第二颗月球探测卫星“嫦娥二号”于2011年6月9日奔向距地球1500000km的深空.用科学记数法表示1500000为( )A、1.5×106 B、0.15×107 C、1.5×107 D、15×1065. 函数 中,自变量x的取值范围是( )A、x≠2 B、x≥2 C、x≤2 D、全体实数6. 将x3﹣4x分解因式的结果是( )A、x(x2﹣4) B、x(x+4)(x﹣4) C、x(x+2)(x﹣2) D、x(x﹣2)27. 函数 的图象是( )A、
A、棱柱 B、棱锥 C、圆柱 D、圆锥3. 下列各式计算正确的是( )A、10a6÷5a2=2a4 B、3 +2 =5 C、2(a2)3=6a6 D、(a﹣2)2=a2﹣44. 我国第二颗月球探测卫星“嫦娥二号”于2011年6月9日奔向距地球1500000km的深空.用科学记数法表示1500000为( )A、1.5×106 B、0.15×107 C、1.5×107 D、15×1065. 函数 中,自变量x的取值范围是( )A、x≠2 B、x≥2 C、x≤2 D、全体实数6. 将x3﹣4x分解因式的结果是( )A、x(x2﹣4) B、x(x+4)(x﹣4) C、x(x+2)(x﹣2) D、x(x﹣2)27. 函数 的图象是( )A、 B、
B、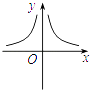 C、
C、 D、
D、 8. 一条公路弯道处是一段圆弧 ,点O是这条弧所在圆的圆心,点C是 的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )
8. 一条公路弯道处是一段圆弧 ,点O是这条弧所在圆的圆心,点C是 的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( ) A、200m B、200 m C、100m D、100 m9. 如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( )
A、200m B、200 m C、100m D、100 m9. 如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 在边长为1的小正方形组成的网格中,有如图所示的A、B两点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率为( )
10. 在边长为1的小正方形组成的网格中,有如图所示的A、B两点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率为( )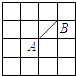 A、 B、 C、 D、11. 如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,阴影部分的面积为( )
A、 B、 C、 D、11. 如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,阴影部分的面积为( )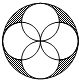 A、π B、2π﹣4 C、 D、 +112.
A、π B、2π﹣4 C、 D、 +112.如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8,则AC•BC的值为( )
 A、14 B、16 C、4 D、16
A、14 B、16 C、4 D、16二、填空题
-
13. 如果向东走3m记作+3m,那么向西走8m记作m.14. 如图是一块梯形铁片的残余部分,量得∠A=100°,则梯形残缺底角的度数是 .
 15. 在平面直角坐标系中,点A(-1,3)关于原点对称点A′的坐标是 .16. 一组数据﹣2、0、﹣3、﹣2、﹣3、1、x的众数是﹣3,则这组数据的中位数是 .17. 化简: .18. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.过点C作CC1⊥AB于C1 , 过点C1作C1C2⊥AC于C2 , 过点C2作C2C3⊥AB于C3 , …,按此作法进行下去,则ACn= .
15. 在平面直角坐标系中,点A(-1,3)关于原点对称点A′的坐标是 .16. 一组数据﹣2、0、﹣3、﹣2、﹣3、1、x的众数是﹣3,则这组数据的中位数是 .17. 化简: .18. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.过点C作CC1⊥AB于C1 , 过点C1作C1C2⊥AC于C2 , 过点C2作C2C3⊥AB于C3 , …,按此作法进行下去,则ACn= .
三、解答题。
-
19. 计算:﹣12+6sin60°﹣ +20110 .20. 解方程: .21. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
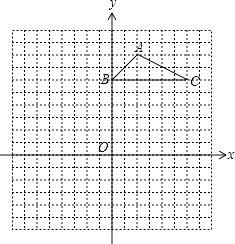 (1)、点A的坐标为 , 点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: .22. 南宁市某校七年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图.已经知A、B两组发言人数直方图高度比为1:5.
(1)、点A的坐标为 , 点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: .22. 南宁市某校七年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图.已经知A、B两组发言人数直方图高度比为1:5.
请结合图中相关的数据回答下列问题:
(1)、A组的人数是多少?本次调查的样本容量是多少?(2)、求出C组的人数并补全直方图.(3)、该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.23.如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠E.
 (1)、请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.(2)、添加了条件后,证明△ABC≌△DEF.24. 南宁市五象新区有长24000m的新建道路要铺上沥青.(1)、写出铺路所需时间t(天)与铺路速度v(m/天)的函数关系式.(2)、负责铺路的工程公司现有的铺路机每天最多能铺路400m,预计最快多少天可以完成铺路任务?(3)、为加快工程进度,公司决定投入不超过400万元的资金,购进10台更先进的铺路机.现有甲、乙两种机器可供选择,其中每种机器的价格和日铺路能力如下表.在原有的铺路机连续铺路40天后,新购进的10台机器加入铺路,公司要求至少比原来预计的时间提前10天完成任务.问有哪几种方案?请你通过计算说明选择哪种方案所用资金最少.
(1)、请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.(2)、添加了条件后,证明△ABC≌△DEF.24. 南宁市五象新区有长24000m的新建道路要铺上沥青.(1)、写出铺路所需时间t(天)与铺路速度v(m/天)的函数关系式.(2)、负责铺路的工程公司现有的铺路机每天最多能铺路400m,预计最快多少天可以完成铺路任务?(3)、为加快工程进度,公司决定投入不超过400万元的资金,购进10台更先进的铺路机.现有甲、乙两种机器可供选择,其中每种机器的价格和日铺路能力如下表.在原有的铺路机连续铺路40天后,新购进的10台机器加入铺路,公司要求至少比原来预计的时间提前10天完成任务.问有哪几种方案?请你通过计算说明选择哪种方案所用资金最少.甲
乙
价格(万元/台)
45
25
每台日铺路能力(m)
50
30
25. 如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B. (1)、求证:直线AB是⊙O的切线.(2)、当AC=1,BE=2,求tan∠OAC的值.26. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)、求证:直线AB是⊙O的切线.(2)、当AC=1,BE=2,求tan∠OAC的值.26. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t. (1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
(1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.