2011年广西柳州市中考数学试卷
试卷更新日期:2017-05-10 类型:中考真卷
一、选择题:
-
1. 在0,﹣2,3, 四个数中,最小的数是( )A、0 B、﹣2 C、3 D、2.
如图,在所标识的角中,互为对顶角的两个角是( )
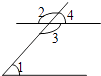 A、∠2和∠3 B、∠1和∠3 C、∠1和∠4 D、∠1和∠23. 方程x2﹣4=0的解是( )A、x=2 B、x=﹣2 C、x=±2 D、x=±44.
A、∠2和∠3 B、∠1和∠3 C、∠1和∠4 D、∠1和∠23. 方程x2﹣4=0的解是( )A、x=2 B、x=﹣2 C、x=±2 D、x=±44.如图的三个图形是某几何体的三视图,则该几何体是( )
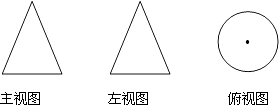 A、正方体 B、圆柱体 C、圆锥体 D、球体5. 若 在实数范围内有意义,则x的取值范围( )A、x≥2 B、x≤2 C、x>2 D、x<26. 如图,A、B、C三点在⊙O上,∠AOB=80°,则∠ACB的大小( )
A、正方体 B、圆柱体 C、圆锥体 D、球体5. 若 在实数范围内有意义,则x的取值范围( )A、x≥2 B、x≤2 C、x>2 D、x<26. 如图,A、B、C三点在⊙O上,∠AOB=80°,则∠ACB的大小( )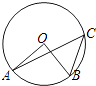 A、40° B、60° C、80° D、100°7.
A、40° B、60° C、80° D、100°7.如图,阴影部分是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,则梯形另外两个底角的度数分别是( )
 A、100°、115° B、100°、65° C、80°、115° D、80°、65°8. 在三角形、四边形、五边形、和正六边形中,是轴对称图形的是( )A、三角形 B、四边形 C、五边形 D、正六边形9. 在平面直角坐标系中,将点A(﹣2,1)向左平移2个单位到点Q,则点Q的坐标为( )A、(﹣2,3) B、(0,1) C、(﹣4,1) D、(﹣4,﹣1)10. 袋子中装有2个红球和4个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机从袋子中摸出1个球,则这个球是红球的概率是( )A、 B、 C、 D、11.
A、100°、115° B、100°、65° C、80°、115° D、80°、65°8. 在三角形、四边形、五边形、和正六边形中,是轴对称图形的是( )A、三角形 B、四边形 C、五边形 D、正六边形9. 在平面直角坐标系中,将点A(﹣2,1)向左平移2个单位到点Q,则点Q的坐标为( )A、(﹣2,3) B、(0,1) C、(﹣4,1) D、(﹣4,﹣1)10. 袋子中装有2个红球和4个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机从袋子中摸出1个球,则这个球是红球的概率是( )A、 B、 C、 D、11.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有( )
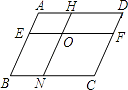 A、12个 B、9个 C、7个 D、5个12. 九(3)班的50名同学进行物理、化学两种实验测试,经最后统计知:物理实验做对的有40人,化学实验做对的有31人,两种实验都做错的有4人,则这两种实验都做对的有( )A、17人 B、21人 C、25人 D、37人
A、12个 B、9个 C、7个 D、5个12. 九(3)班的50名同学进行物理、化学两种实验测试,经最后统计知:物理实验做对的有40人,化学实验做对的有31人,两种实验都做错的有4人,则这两种实验都做对的有( )A、17人 B、21人 C、25人 D、37人二、填空题
-
13. 计算:2×(﹣3)= .14. 单项式3x2y3的系数是 .15. 把方程2x+y=3改写成用含x的式子表示y的形式,得y= .16. 不等式组 的解集是 .17. 如图,要测量的A、C两点被池塘隔开,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得E、F两点间的距离等于23米,则A、C两点间的距离米.
 18. 如图,⊙O的半径为5,直径AB⊥CD,以B为圆心,BC长为半径作 ,则 与 围成的新月形ACDE(阴影部分)的面积为 .
18. 如图,⊙O的半径为5,直径AB⊥CD,以B为圆心,BC长为半径作 ,则 与 围成的新月形ACDE(阴影部分)的面积为 .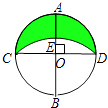
三、解答题
-
19. 化简:2a(a﹣ )+a.20. 如图,AB=AC,点E、F分别是AB、AC的中点,求证:△AFB≌△AEC.
 21. 某班“环卫小组”为了宣传环保的重要性,随机调查了本班10名同学的家庭在同一天内丢弃垃圾的情况.经统计,丢垃圾的质量如下(单位:千克):
21. 某班“环卫小组”为了宣传环保的重要性,随机调查了本班10名同学的家庭在同一天内丢弃垃圾的情况.经统计,丢垃圾的质量如下(单位:千克):2 3 3 4 4 3 5 3 4 5
根据上述数据,回答下列问题:
(1)、写出上述10个数据的中位数、众数;(2)、若这个班共有50名同学,请你根据上述数据的平均数,估算这50个家庭在这一天丢弃垃圾的质量.22. 在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据 ≈1.73).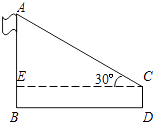 23. 某校为了创建书香校园,去年又购进了一批图书.经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.(1)、求去年购进的文学书和科普书的单价各是多少元?(2)、若今年文学书和科普书的单价和去年相比保持不变,该校打算用1000元再购进一批文学书和科普书,问购进文学书55本后至多还能购进多少本科普书?24. 如图,直线y=kx+k(k≠0)与双曲线y= 在第一象限内相交于点M,与x轴交于点A.
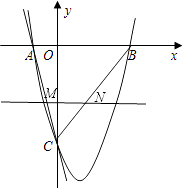
23. 某校为了创建书香校园,去年又购进了一批图书.经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.(1)、求去年购进的文学书和科普书的单价各是多少元?(2)、若今年文学书和科普书的单价和去年相比保持不变,该校打算用1000元再购进一批文学书和科普书,问购进文学书55本后至多还能购进多少本科普书?24. 如图,直线y=kx+k(k≠0)与双曲线y= 在第一象限内相交于点M,与x轴交于点A.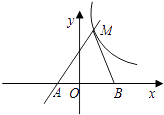 (1)、求m的取值范围和点A的坐标;(2)、若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.25. 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)、求m的取值范围和点A的坐标;(2)、若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.25. 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.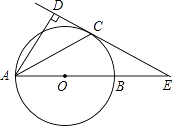 (1)、求证:直线CD为⊙O的切线;(2)、当AB=2BE,且CE= 时,求AD的长.26. 如图,一次函数y=﹣4x﹣4的图象与x轴、y轴分别交于A、C两点,抛物线y= x2+bx+c的图象经过A、C两点,且与x轴交于点B.
(1)、求证:直线CD为⊙O的切线;(2)、当AB=2BE,且CE= 时,求AD的长.26. 如图,一次函数y=﹣4x﹣4的图象与x轴、y轴分别交于A、C两点,抛物线y= x2+bx+c的图象经过A、C两点,且与x轴交于点B.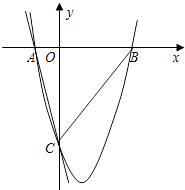 (1)、求抛物线的函数表达式;(2)、设抛物线的顶点为D,求四边形ABDC的面积;
(1)、求抛物线的函数表达式;(2)、设抛物线的顶点为D,求四边形ABDC的面积;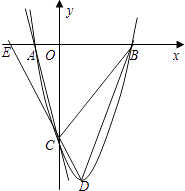 (3)、作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
(3)、作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.