2011年广西来宾市中考数学试卷
试卷更新日期:2017-05-10 类型:中考真卷
一、选择题.
-
1. 据国家统计局2011年4月28日发布的《2011年第六次全国人口普查主要数据公报(第一号)》,总人口为1370536875人,这一数字用科学记数法表示为( )(保留四个有效数字)A、1.37×109 B、1.37×108 C、1.371×109 D、1.371×1082. 圆柱的侧面展开图形是( )A、圆 B、矩形 C、梯形 D、扇形3. 使函数y= 有意义的自变量x的取值范围是( )A、x≠﹣1 B、x≠1 C、x≠1且x≠0 D、x≠﹣1且x≠04. 已知⊙O1和⊙O2的半径分别是4和5,且O1O2=8,则这两个圆的位置关系是( )A、外离 B、外切 C、相交 D、内含5. 已知一个三角形的两边长分别是2和3,则下列数据中,可作为第三边的长的是( )A、1 B、3 C、5 D、76. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则∠A的余弦值为( )A、 B、 C、 D、7. 下列计算正确的是( )A、(a+b)2=a2+b2 B、(﹣2a)3=﹣6a3 C、(a2b)3=a5b3 D、(﹣a)7÷(﹣a)3=a48. 不等式组 的解集在数轴上可表示为 ( )A、
 B、
B、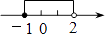 C、
C、 D、
D、 9. 如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )A、六边形 B、五边形 C、四边形 D、三角形10. 计算 ﹣ 的结果是( )A、﹣ B、 C、 D、11. 在直角梯形ABCD中(如图所示),已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )
9. 如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )A、六边形 B、五边形 C、四边形 D、三角形10. 计算 ﹣ 的结果是( )A、﹣ B、 C、 D、11. 在直角梯形ABCD中(如图所示),已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( ) A、3 B、5 C、6 D、812. 如图,在△ABC中,已知∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积( )
A、3 B、5 C、6 D、812. 如图,在△ABC中,已知∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积( ) A、1﹣ B、 C、1﹣ D、2﹣
A、1﹣ B、 C、1﹣ D、2﹣二、填空题.
-
13. ﹣2011的相反数是 .14. 在▱ABCD中,已知∠A=110°,则∠D=°.15. 分解因式:1﹣x2= .16. m千克浓度为a%的某溶液中溶剂的质量为千克.17. 已知一元二次方程x2+mx﹣2=0的两个实数根分别为x1 , x2 , 则x1•x2= .18. 某校八年级共240名学生参加某次数学测试,教师从中随机抽取了40名学生的成绩进行统计,共有12名学生成绩达到优秀等级,根据上述数据估算该校八年级学生在这次数学测试中达到优秀的人数大约有人.
三、解答题.
-
19. 计算:|﹣3|﹣ ﹣( )0+32 .20. 小明对所在班级的“小书库”进行了分类统计,并制作了如下的统计图表:
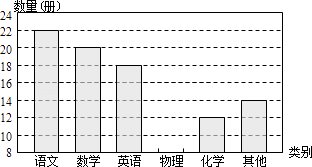
根据上述信息,完成下列问题:
(1)、图书总册数是多少册,a是多少册;(2)、请将条形统计图补充完整;类别
语文
数学
英语
物理
化学
其他
数量(册)
22
20
18
a
12
14
频率
0.14
(3)、数据22,20,18,a,12,14中的众数是多少,极差是多少;(4)、小明从这些书中任意拿一册来阅读,求他恰好拿到数学或英语书的概率.21. 某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.(1)、求第一次每个书包的进价是多少元?(2)、若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包全部按同一标准一次性打折销售,但要求这次的利润不少于480元,问最低可打几折?22. 如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E. (1)、用圆规和直尺在图中作出AB的垂直平分线DE,并连接BD;(2)、证明:△ABC∽△BDC.23. 已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)、用圆规和直尺在图中作出AB的垂直平分线DE,并连接BD;(2)、证明:△ABC∽△BDC.23. 已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2), (1)、求这两个函数的关系式;(2)、观察图象,写出使得y1>y2成立的自变量x的取值范围;(3)、如果点C与点A关于x轴对称,求△ABC的面积.24. 已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)、求这两个函数的关系式;(2)、观察图象,写出使得y1>y2成立的自变量x的取值范围;(3)、如果点C与点A关于x轴对称,求△ABC的面积.24. 已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点, (1)、如果动点E、F满足BE=CF(如图1):
(1)、如果动点E、F满足BE=CF(如图1):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)、如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.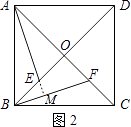 25. 如图,半径为1的⊙M经过直角坐标系的原点O,且分别与x轴正半轴、y轴正半轴交于点A、B,∠OMA=60°,过点B的切线交x轴负半轴于点C,抛物线过点A、B、C.
25. 如图,半径为1的⊙M经过直角坐标系的原点O,且分别与x轴正半轴、y轴正半轴交于点A、B,∠OMA=60°,过点B的切线交x轴负半轴于点C,抛物线过点A、B、C. (1)、求点A、B的坐标;(2)、求抛物线的函数关系式;(3)、若点D为抛物线对称轴上的一个动点,问是否存在这样的点D,使得△BCD是等腰三角形?若存在,求出符合条件的点D的坐标;若不存在,请说明理由.
(1)、求点A、B的坐标;(2)、求抛物线的函数关系式;(3)、若点D为抛物线对称轴上的一个动点,问是否存在这样的点D,使得△BCD是等腰三角形?若存在,求出符合条件的点D的坐标;若不存在,请说明理由.