2012年贵州省遵义市中考数学试卷

试卷更新日期：2017-05-10 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣（﹣2）的值是（）

A、﹣2 B、2 C、±2 D、4

查看试题解析
2. 据有关资料显示，2011年遵义市全年财政总收入202亿元，将202亿用科学记数法可表示（）

A、2.02×10² B、202×10⁸ C、2.02×10⁹ D、2.02×10¹⁰

查看试题解析
3. 把一张正方形纸片如图①、图②对折两次后，再按如图③挖去一个三角形小孔，则展开后图形是（）

A、 B、 C、 D、

查看试题解析
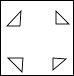4. 下列运算中，正确的是（）

A、3a﹣a=3 B、a²+a³=a⁵ C、（﹣2a）³=﹣6a³ D、ab²÷a=b²

查看试题解析
5. 某班六名同学体能测试成绩（分）如下：80，90，75，75，80，80，对这组数据表述错误的是（）

A、众数是80 B、极差是15 C、平均数是80 D、中位数是75

查看试题解析
6. 如图，数轴上表示某不等式组的解集，则这个不等式组可能是（）

A、 ${\begin{matrix} x + 1 \geq 0 \\ 2 - x \geq 0 \end{matrix}$ B、 ${\begin{matrix} x + 1 \leq 0 \\ 2 - x \geq 0 \end{matrix}$ C、 ${\begin{matrix} x + 1 \leq 0 \\ x - 2 \geq 0 \end{matrix}$ D、 ${\begin{matrix} x + 1 \geq 0 \\ x - 2 \geq 0 \end{matrix}$

查看试题解析
7. 如图，在△ABC中，EF∥BC， $\frac{A E}{E B}$ = $\frac{1}{2}$ ，S_四边形_BCFE=8，则S_△_ABC=（）

A、9 B、10 C、12 D、13

查看试题解析
8. 如图，从边长为（a+1）cm的正方形纸片中剪去一个边长为（a﹣1）cm的正方形（a＞1），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则该矩形的面积是（）

A、2cm² B、2acm² C、4acm² D、（a²﹣1）cm²

查看试题解析
9. 如图，半径为1cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为（）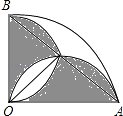

A、πcm² B、 $\frac{2}{3}$ πcm² C、 $\frac{1}{2}$ cm² D、 $\frac{2}{3}$ cm²

查看试题解析
10. 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（）

A、3 $\sqrt{2}$ B、2 $\sqrt{6}$ C、2 $\sqrt{5}$ D、2 $\sqrt{3}$

查看试题解析

二、填空题

11. 计算： $\sqrt{32}$ ﹣ $\sqrt{2}$ = ．

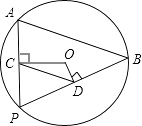
查看试题解析
12. 一个等腰三角形的两条边分别为4cm和8cm，则这个三角形的周长为．

查看试题解析
13. 2012•晋江市）已知x+y=﹣5，xy=6，则x²+y²= ．

查看试题解析
14. 如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为．

查看试题解析
15. 如图，将边长为 $\sqrt{2}$ cm的正方形ABCD沿直线l向右翻动（不滑动），当正方形连续翻动6次后，正方形的中心O经过的路线长是cm．（结果保留π）

查看试题解析
16. 猜数字游戏中，小明写出如下一组数： $\frac{2}{5}$ ， $\frac{4}{7}$ ， $\frac{8}{11}$ ， $\frac{16}{19}$ ， $\frac{32}{35}$ …，小亮猜想出第六个数字是 $\frac{64}{67}$ ，根据此规律，第n个数是．

查看试题解析
17. 在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种．

查看试题解析
18.
如图，平行四边形ABCD的顶点A、C在双曲线y₁=﹣ $\frac{k_{1}}{x}$ 上，B、D在双曲线y₂= $\frac{k_{2}}{x}$ 上，k₁=2k₂（k₁＞0），AB∥y轴，S_▱ABCD=24，则k₁= ．

查看试题解析

三、解答题

19. 计算：（﹣1）¹⁰¹+（π﹣3）⁰+（ $\frac{1}{2}$ ）^﹣¹﹣ $\sqrt{{(1 - \sqrt{2})}^{2}}$ ．

查看试题解析
20. 化简分式（ $\frac{x}{x - 1}$ ﹣ $\frac{x}{x^{2} - 1}$ ）÷ $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，并从﹣1≤x≤3中选一个你认为合适的整数x代入求值．

查看试题解析
21. 为促进我市经济的快速发展，加快道路建设，某高速公路建设工程中需修隧道AB，如图，在山外一点C测得BC距离为200m，∠CAB=54°，∠CBA=30°，求隧道AB的长．（参考数据：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38， $\sqrt{3}$ ≈1.73，精确到个位）

查看试题解析
22. 如图，4张背面完全相同的纸牌（用①、②、③、④表示），在纸牌的正面分别写有四个不同的条件，小明将这4张纸牌背面朝上洗匀后，先随机摸出一张（不放回），再随机摸出一张．

(1)、用树状图（或列表法）表示两次摸牌出现的所有可能结果；

(2)、以两次摸出牌上的结果为条件，求能判断四边形ABCD是平行四边形的概率．

查看试题解析
23. 根据遵义市统计局发布的2011年遵义市国民经济和社会发展统计公报相关数据，我市2011年社会消费品总额按城乡划分绘制统计图①，2010年与2011年社会消费品销售额按行业划分绘制条形统计图②，根据图中信息回答下列问题：

(1)、图①中“乡村消费品销售额”的圆心角是度，乡村消费品销售额为亿元；

(2)、2010年到2011年间，批发业、零售业、餐饮住宿业中销售额增长的百分数最大的行业是；

(3)、预计2013年我市的社会消品总销售额到达504亿元，求我市2011﹣2013年社会消费品销售总额的年平均增长率．

查看试题解析
24. 如图，△OAC中，以O为圆心，OA为半径作⊙O，作OB⊥OC交⊙O于B，垂足为O，连接AB交OC于点D，∠CAD=∠CDA．

(1)、判断AC与⊙O的位置关系，并证明你的结论；

(2)、若OA=5，OD=1，求线段AC的长．

查看试题解析
25. 为了促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中折线反映了每户每月用电电费y（元）与用电量x（度）间的函数关系式．

(1)、根据图象，阶梯电价方案分为三个档次，填写下表：
档次
第一档
第二档
第三档
每月用电量x（度）
0＜x≤140

(2)、小明家某月用电120度，需交电费元；

(3)、求第二档每月电费y（元）与用电量x（度）之间的函数关系式；

(4)、在每月用电量超过230度时，每多用1度电要比第二档多付电费m元，小刚家某月用电290度，交电费153元，求m的值．

查看试题解析
26. 如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．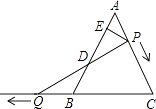

(1)、当∠BQD=30°时，求AP的长；

(2)、当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

查看试题解析
27.
如图，已知抛物线y=ax²+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，﹣ $\sqrt{3}$ ）．

(1)、求抛物线的函数解析式及点A的坐标；

(2)、在抛物线上求点P，使S_△_POA=2S_△_AOB；

(3)、在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．

查看试题解析

档次	第一档	第二档	第三档
每月用电量x（度）	0＜x≤140