2013年福建省福州市中考数学试卷
试卷更新日期:2017-05-10 类型:中考真卷
一、选择题
-
1. 2的倒数是( )A、 B、﹣ C、2 D、﹣22. 如图,OA⊥OB,若∠1=40°,则∠2的度数是( )
 A、20° B、40° C、50° D、60°3. 2012年12月13日,嫦娥二号成功飞抵距地球约700万公里远的深空,7 000 000用科学记数法表示为( )A、7×105 B、7×106 C、70×106 D、7×1074. 下列立体图形中,俯视图是正方形的是( )A、
A、20° B、40° C、50° D、60°3. 2012年12月13日,嫦娥二号成功飞抵距地球约700万公里远的深空,7 000 000用科学记数法表示为( )A、7×105 B、7×106 C、70×106 D、7×1074. 下列立体图形中,俯视图是正方形的是( )A、 B、
B、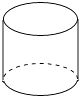 C、
C、 D、
D、 5. 下列一元二次方程有两个相等实数根的是( )A、x2+3=0 B、x2+2x=0 C、(x+1)2=0 D、(x+3)(x﹣1)=06. 不等式1+x<0的解集在数轴上表示正确的是( )A、
5. 下列一元二次方程有两个相等实数根的是( )A、x2+3=0 B、x2+2x=0 C、(x+1)2=0 D、(x+3)(x﹣1)=06. 不等式1+x<0的解集在数轴上表示正确的是( )A、 B、
B、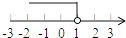 C、
C、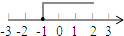 D、
D、 7. 下列运算正确的是( )A、a•a2=a3 B、(a2)3=a5 C、 D、a3÷a3=a8. 如图,已知△ABC,以点B为圆心,AC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在BC异侧,连结AD,量一量线段AD的长,约为( )
7. 下列运算正确的是( )A、a•a2=a3 B、(a2)3=a5 C、 D、a3÷a3=a8. 如图,已知△ABC,以点B为圆心,AC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在BC异侧,连结AD,量一量线段AD的长,约为( ) A、2.5cm B、3.0cm C、3.5cm D、4.0cm9. 袋中有红球4个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )A、3个 B、不足3个 C、4个 D、5个或5个以上10.
A、2.5cm B、3.0cm C、3.5cm D、4.0cm9. 袋中有红球4个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )A、3个 B、不足3个 C、4个 D、5个或5个以上10.A,B两点在一次函数图象上的位置如图所示,两点的坐标分别为A(x+a,y+b),B(x,y),下列结论正确的是( )
 A、a>0 B、a<0 C、b=0 D、ab<0
A、a>0 B、a<0 C、b=0 D、ab<0二、填空题
-
11. 计算: = .12. 矩形的外角和等于度.13. 某校女子排球队队员的年龄分布如下表:
年龄
13
14
15
人数
4
7
4
则该校女子排球队队员的平均年龄是岁.
14. 已知实数a,b满足a+b=2,a﹣b=5,则(a+b)3•(a﹣b)3的值是 .15. 如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是 .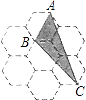
三、解答题
-
16.(1)、计算: ;(2)、化简:(a+3)2+a(4﹣a)17.
 (1)、如图,AB平分∠CAD,AC=AD,求证:BC=BD;(2)、列方程解应用题
(1)、如图,AB平分∠CAD,AC=AD,求证:BC=BD;(2)、列方程解应用题把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本,这个班有多少学生?
18. 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高情况分组表(单位:cm)
组别
身高
A
x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
x≥170
根据图表提供的信息,回答下列问题:
 (1)、样本中,男生的身高众数在组,中位数在组;(2)、样本中,女生身高在E组的人数有人;(3)、已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?19. 如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)、样本中,男生的身高众数在组,中位数在组;(2)、样本中,女生身高在E组的人数有人;(3)、已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?19. 如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD. (1)、△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度;(2)、连结AD,交OC于点E,求∠AEO的度数.20. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=
(1)、△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度;(2)、连结AD,交OC于点E,求∠AEO的度数.20. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE= (1)、求证:BC是⊙O的切线;(2)、求 的长.21.
(1)、求证:BC是⊙O的切线;(2)、求 的长.21.如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为 ,设AB=x,AD=y
 (1)、求y与x的函数关系式;(2)、若∠APD=45°,当y=1时,求PB•PC的值;(3)、若∠APD=90°,求y的最小值.22. 我们知道,经过原点的抛物线的解析式可以是y=ax2+bx(a≠0)(1)、对于这样的抛物线:
(1)、求y与x的函数关系式;(2)、若∠APD=45°,当y=1时,求PB•PC的值;(3)、若∠APD=90°,求y的最小值.22. 我们知道,经过原点的抛物线的解析式可以是y=ax2+bx(a≠0)(1)、对于这样的抛物线:当顶点坐标为(1,1)时,a=;
当顶点坐标为(m,m),m≠0时,a与m之间的关系式是
(2)、继续探究,如果b≠0,且过原点的抛物线顶点在直线y=kx(k≠0)上,请用含k的代数式表示b;(3)、现有一组过原点的抛物线,顶点A1 , A2 , …,An在直线y=x上,横坐标依次为1,2,…,n(为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1 , B2 , …,Bn , 以线段AnBn为边向右作正方形AnBnCnDn , 若这组抛物线中有一条经过Dn , 求所有满足条件的正方形边长.