广西桂林市,贺州市,崇左市2019年高三下学期理数3月联合调研考试试卷
试卷更新日期:2019-04-17 类型:高考模拟
一、单选题
-
1. 设集合 为全集,集合 ,则 ( )A、 B、 C、 D、2. 已知复数 ,则 ( )A、1 B、 C、 D、133. 以双曲线 右焦点为圆心,且与双曲线的渐近线相切的圆的方程为( )A、 B、 C、 D、4. 某几何体的三视图如图所示,则该几何体的表面积等于( )
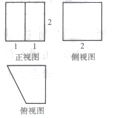 A、10 B、13 C、 D、5. 某市气象部门根据2018年各月的每天最高气温平均值与最低气温平均值(单位: )数据,绘制如下拆线图:
A、10 B、13 C、 D、5. 某市气象部门根据2018年各月的每天最高气温平均值与最低气温平均值(单位: )数据,绘制如下拆线图:
那么,下列叙述错误的是( )
A、各月最高气温平均值与最低气温平均值总体呈正相关 B、全年中,2月份的最高气温平均值与最低气温平均值的差值最大 C、全年中各月最低气温平均值不高于 的月份有5个 D、从2018年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势6. 的展开式中的一次项系数是( )A、-20 B、14 C、20 D、357. 已知等比数列 的前 项和 ,则 ( )A、 B、3 C、6 D、98. 函数 的大致图像为( )A、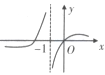 B、
B、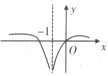 C、
C、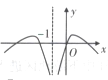 D、
D、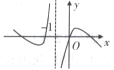 9. 已知定义在 上的奇函数 满足 ,且当 时, ,若 ,则实数 ( )A、 B、 C、 D、10. 已知函数 ,若 ,且 ,则函数 取得最大值时 的可能值为( )A、 B、 C、 D、11. 2018年9月24日,英国数学家M.F阿帝亚爵在“海德堡论坛”展示了他“证明”黎曼猜想的过程,引起数学界震动,黎曼猜想来源于一些特殊数列求和.记无穷数列 的各项的和 ,那么下列结论正确的是( )A、 B、 C、 D、12. 已知 为椭圆 上三个不同的点, 为坐标原点,若 ,则 的面积为( )A、 B、 C、 D、
9. 已知定义在 上的奇函数 满足 ,且当 时, ,若 ,则实数 ( )A、 B、 C、 D、10. 已知函数 ,若 ,且 ,则函数 取得最大值时 的可能值为( )A、 B、 C、 D、11. 2018年9月24日,英国数学家M.F阿帝亚爵在“海德堡论坛”展示了他“证明”黎曼猜想的过程,引起数学界震动,黎曼猜想来源于一些特殊数列求和.记无穷数列 的各项的和 ,那么下列结论正确的是( )A、 B、 C、 D、12. 已知 为椭圆 上三个不同的点, 为坐标原点,若 ,则 的面积为( )A、 B、 C、 D、二、填空题
-
13. 已知 , , ,则向量 在 方向上的投影为 .14. 某校今年计划招聘女教师 人,男教师 人,若 、 满足 则该学校今年计划招聘的教师人数最大值为 .15. 在三棱锥 中, , , , ,则三棱锥 外接球的体积的最小值为 .16. 已知函数 ,函数 有三个不同的零点 , , ,则 的取值范围是 .
三、解答题
-
17. 在 中, 分别是角 所对的边,已知 ,且满足 .(1)、求角 和边 的大小;(2)、求 面积的最大值.18. 每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区2009~2018年10年间梅雨季节的降雨量(单位: )的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
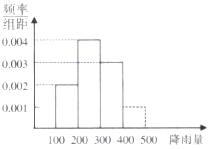 (1)、假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350 的概率;(2)、老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元.而乙品种杨梅的亩产量 ( /亩)与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为 (元/ ),请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润 (万元)的期望更大?并说明理由.
(1)、假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350 的概率;(2)、老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元.而乙品种杨梅的亩产量 ( /亩)与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为 (元/ ),请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润 (万元)的期望更大?并说明理由.降雨量
亩产量
500
700
600
400
19. 已知三棱柱 中, , , , .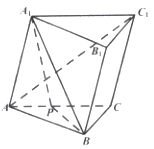 (1)、求证:平面 平面 ;(2)、若 , 为线段 上一点,且平面 和平面 所成角的余弦值为 ,求 的值.20. 已知抛物线 ,过点 的直线 交抛物线于 、 两点,设 为坐标原点, ,且 .(1)、求 的值;(2)、若 , , 的面积成等比数列,求直线 的方程.
(1)、求证:平面 平面 ;(2)、若 , 为线段 上一点,且平面 和平面 所成角的余弦值为 ,求 的值.20. 已知抛物线 ,过点 的直线 交抛物线于 、 两点,设 为坐标原点, ,且 .(1)、求 的值;(2)、若 , , 的面积成等比数列,求直线 的方程.