广东省深圳市2019届高三第一次(2月)调研考试数学理试题
试卷更新日期:2019-04-17 类型:高考模拟
一、单选题
-
1. 复数 的共轭复数是( )A、 B、 C、 D、2. 已知集合 , ,则 ( )A、 B、 C、 D、3. 设 为等差数列 的前 项和.若 , ,则 的公差为( )A、-2 B、-1 C、1 D、24. 已知某产品的销售额 与广告费用 之间的关系如下表:
(单位:万元)
0
1
2
3
4
(单位:万元)
10
15
20
30
35
若求得其线性回归方程为 ,则预计当广告费用为6万元时的销售额为( )
A、42万元 B、45万元 C、48万元 D、51万元5. 如图所示,网格纸上小正方形的边长为1,粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图,则该几何体的体积为( ) A、72 B、64 C、48 D、326. 已知直线 是函数 与的图象的一条对称轴,为了得到函数 的图象,可把函数 的图象( )A、向左平行移动 个单位长度 B、向右平行移动 个单位长度 C、向左平行移动 个单位长度 D、向右平行移动 个单位长度7. 在 中, , , 为 的中点,则 ( )A、-2 B、-1 C、0 D、18. 古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出已知线段的黄金分割点,具体方法如下:(l)取线段 ,过点 作 的垂线,并 用圆规在垂线上截取 ,连接 ;(2)以 为圆心, 为半径画弧,交 于点 ;(3)以 为圆心,以 为半径画弧,交 于点 .则点 即为线段 的黄金分割点.若在线段 上随机取一点F,则使得 的概率约为( )(参考数据: )
A、72 B、64 C、48 D、326. 已知直线 是函数 与的图象的一条对称轴,为了得到函数 的图象,可把函数 的图象( )A、向左平行移动 个单位长度 B、向右平行移动 个单位长度 C、向左平行移动 个单位长度 D、向右平行移动 个单位长度7. 在 中, , , 为 的中点,则 ( )A、-2 B、-1 C、0 D、18. 古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出已知线段的黄金分割点,具体方法如下:(l)取线段 ,过点 作 的垂线,并 用圆规在垂线上截取 ,连接 ;(2)以 为圆心, 为半径画弧,交 于点 ;(3)以 为圆心,以 为半径画弧,交 于点 .则点 即为线段 的黄金分割点.若在线段 上随机取一点F,则使得 的概率约为( )(参考数据: )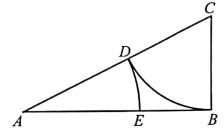 A、0.236 B、0.382 C、0.472 D、0.6189. 已知偶函数 的图象经过点 ,且当 时,不等式 恒成立,则使得 成立的 的取值范围是( )A、 B、 C、 D、10. 已知直线 与双曲线 交于 两点,以 为直径的圆恰好经过双曲线的右焦点 ,若 的面积为 ,则双曲线的离心率为( )A、 B、 C、2 D、11. 已知 为球 的球面上的三个定点, , , 为球 的球面上的动点,记三棱锥 的体积为 ,三棱锥 的体积为 ,若 的最大值为3,则球 的表面积为( )A、 B、 C、 D、12. 若关于 的不等式 有正整数解,则实数 的最小值为( )A、6 B、7 C、8 D、9
A、0.236 B、0.382 C、0.472 D、0.6189. 已知偶函数 的图象经过点 ,且当 时,不等式 恒成立,则使得 成立的 的取值范围是( )A、 B、 C、 D、10. 已知直线 与双曲线 交于 两点,以 为直径的圆恰好经过双曲线的右焦点 ,若 的面积为 ,则双曲线的离心率为( )A、 B、 C、2 D、11. 已知 为球 的球面上的三个定点, , , 为球 的球面上的动点,记三棱锥 的体积为 ,三棱锥 的体积为 ,若 的最大值为3,则球 的表面积为( )A、 B、 C、 D、12. 若关于 的不等式 有正整数解,则实数 的最小值为( )A、6 B、7 C、8 D、9二、填空题
-
13. 设 满足约束条件 ,则目标函数 的最大值为 .14. 若 的展开式中各项系数之和为32,则展开式中 的系数为 .15. 已知点 在 轴上,点 是抛物线 的焦点,直线 与抛物线交于 , 两点,若点 为线段 的中点,且 ,则 .
三、解答题
-
16. 如图,在平面四边形 中, 与 为其对角线,已知 ,且 .
 (1)、若 平分 ,且 ,求 的长;(2)、若 ,求 的长.17. 如图,在四棱锥 中,底面 是边长为1的菱形, , , 为 的中点, 为 的中点,点 在线段 上,且 .
(1)、若 平分 ,且 ,求 的长;(2)、若 ,求 的长.17. 如图,在四棱锥 中,底面 是边长为1的菱形, , , 为 的中点, 为 的中点,点 在线段 上,且 .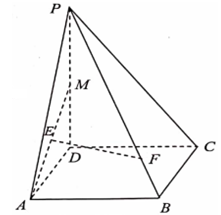 (1)、求证: 平面 ;(2)、若平面 底面 ,且 ,求平面 与平面 所成锐二面角的余弦值.18. 在平面直角坐标系 中, 椭圆 的中心在坐标原点 ,其右焦点为 ,且点 在椭圆 上.
(1)、求证: 平面 ;(2)、若平面 底面 ,且 ,求平面 与平面 所成锐二面角的余弦值.18. 在平面直角坐标系 中, 椭圆 的中心在坐标原点 ,其右焦点为 ,且点 在椭圆 上.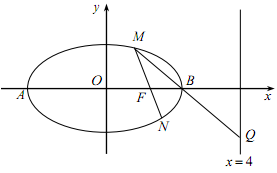 (1)、求椭圆 的方程;(2)、设椭圆的左、右顶点分别为 、 、 是椭圆上异于 , 的任意一点,直线 交椭圆 于另一点 ,直线 交直线 于 点, 求证: , , 三点在同一条直线上.19. 某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:
(1)、求椭圆 的方程;(2)、设椭圆的左、右顶点分别为 、 、 是椭圆上异于 , 的任意一点,直线 交椭圆 于另一点 ,直线 交直线 于 点, 求证: , , 三点在同一条直线上.19. 某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示: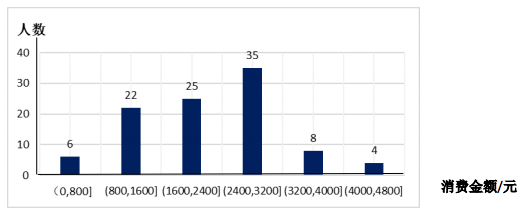 (1)、将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;(2)、针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
(1)、将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;(2)、针对这些消费者,该健身机构今年欲实施入会制,详情如下表:会员等级
消费金额
普通会员
2000
银卡会员
2700
金卡会员
3200
预计去年消费金额在 内的消费者今年都将会申请办理普通会员,消费金额在 内的消费者都将会申请办理银卡会员,消费金额在 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案 1:按分层抽样从普通会员, 银卡会员, 金卡会员中总共抽取 25 位“幸运之星”给予奖励: 普通会员中的“幸运之星”每人奖励 500 元; 银卡会员中的“幸运之星”每人奖励 600 元; 金卡会员中的“幸运之星”每人奖励 800 元.
方案 2:每位会员均可参加摸奖游戏,游戏规则如下:从-个装有 3 个白球、 2 个红球(球只有颜色不同)的箱子中, 有放回地摸三次球,每次只能摸-个球.若摸到红球的总数消费金额/元为 2,则可获得 200 元奖励金; 若摸到红球的总数为 3,则可获得 300 元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏;每位银卡会员均可参加 2 次摸奖游戏;每位金卡会员均可参加 3 次摸奖游戏(每次摸奖的结果相互独立) .
以方案 2 的奖励金的数学期望为依据,请你预测哪-种方案投资较少?并说明理由.
20. 已知函数 ,其定义域为 .(其中常数 ,是自然对数的底数)(1)、求函数 的递增区间;(2)、若函数 为定义域上的增函数,且 ,证明: .