福建省龙岩市2019届高三下学期理数教学质量检测试卷
试卷更新日期:2019-04-17 类型:高考模拟
一、单选题
-
1. 已知 为虚数单位,则 的值为( )A、 B、 C、 D、2. 已知 ,则 ( )A、 B、 C、 D、3. 已知等差数列 的公差为 ,若 成等比数列,则数列 的前8 项和为( )A、-20 B、-18 C、-8 D、-104. 如果执行下面的程序框图,输入正整数 ,且满足 ,那么输出的 等于( )
 A、 B、 C、 D、5. 已知实数 , 满足不等式组 ,则 的取值范围为( )A、 B、 C、 D、6. 已知双曲线 和双曲线 焦距相等,离心率分别为 、 ,若 ,则下列结论正确的是( )A、 和 离心率相等 B、 和 渐近线相同 C、 和 实轴长相等 D、 和 虚轴长相等7. 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 ( )
A、 B、 C、 D、5. 已知实数 , 满足不等式组 ,则 的取值范围为( )A、 B、 C、 D、6. 已知双曲线 和双曲线 焦距相等,离心率分别为 、 ,若 ,则下列结论正确的是( )A、 和 离心率相等 B、 和 渐近线相同 C、 和 实轴长相等 D、 和 虚轴长相等7. 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 ( ) A、 B、 C、 D、8. 如图, 和 是圆 两条互相垂直的直径,分别以 , , , 为直径作四个圆,在圆 内随机取一点,则此点取自阴影部分的概率是( )
A、 B、 C、 D、8. 如图, 和 是圆 两条互相垂直的直径,分别以 , , , 为直径作四个圆,在圆 内随机取一点,则此点取自阴影部分的概率是( )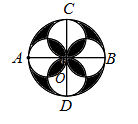 A、 B、 C、 D、9. 已知函数 在区间 上单调,则 的取值范围为 ( )A、 B、 C、 D、10. 设 , ,当 取最小值时 的值为( )A、2 B、3 C、4 D、511. 如图,已知正方体 的棱长为4, 是 的中点,点 在侧面 内,若 ,则 面积的最小值为( )
A、 B、 C、 D、9. 已知函数 在区间 上单调,则 的取值范围为 ( )A、 B、 C、 D、10. 设 , ,当 取最小值时 的值为( )A、2 B、3 C、4 D、511. 如图,已知正方体 的棱长为4, 是 的中点,点 在侧面 内,若 ,则 面积的最小值为( ) A、8 B、4 C、 D、12. 已知数列 各项均为整数,共有7项,且满足 , ,其中 , ( 为常数且 ).若满足上述条件的不同数列个数共有15个,则 的值为( )A、1 B、3 C、5 D、7
A、8 B、4 C、 D、12. 已知数列 各项均为整数,共有7项,且满足 , ,其中 , ( 为常数且 ).若满足上述条件的不同数列个数共有15个,则 的值为( )A、1 B、3 C、5 D、7二、填空题
-
13. 已知向量 , 的夹角为 , , ,则 .14. 若 的展开式中 项的系数为16,则实数 = .15. 已知抛物线 的焦点为 ,其准线与 轴的交点为 ,过点 作直线与抛物线交于 两点.若以 为直径的圆过点 ,则 的值为 .16. 已知 ,若 的图像和 的图像有四个不同的公共点,则实数 的取值范围是 .
三、解答题
-
17. 在 中,内角 , , 所对的边分别为 , , ,已知 .
(Ⅰ)求角 的大小;
(Ⅱ)设 为 中点,若 ,求 面积的取值范围.
18. 如图,已知四边形 是边长为2的菱形,且 , , , ,点 是线段 上的一点. 为线段 的中点.
(Ⅰ)若 ⊥ 于 且 ,证明: 平面 ;
(Ⅱ)若 , ,求二面角 的余弦值.
19. 已知椭圆 的方程为 ,点 为长轴的右端点. 为椭圆 上关于原点对称的两点.直线 与直线 的斜率 满足: .(Ⅰ)求椭圆 的标准方程;
(Ⅱ)若直线 与圆 相切,且与椭圆 相交于 两点,求证:以线段 为直径的圆恒过原点.
20. 某医院为筛查某种疾病,需要检验血液是否为阳性,现有 ( )份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验 次;(2)混合检验,将其中 ( 且 )份血液样本分别取样混合在一起检验.若检验结果为阴性,这 份的血液全为阴性,因而这 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这 份血液究竟哪几份为阳性,就要对这 份再逐份检验,此时这 份血液的检验次数总共为 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为 .(Ⅰ)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.
(Ⅱ)现取其中 ( 且 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为 ,采用混合检验方式,样本需要检验的总次数为
(ⅰ)试运用概率统计的知识,若 ,试求 关于 的函数关系式 ;
(ⅱ)若 ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求 的最大值.
参考数据: , , , ,