广东省惠州市惠城区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期：2019-04-16 类型：期末考试
一、选择题（共30分）
-
1. 在正方形、矩形、菱形、平行四边形中，其中是中心对称图形的个数为（ ）A、1 B、2 C、3 D、42. 如图，四边形ABCD是⊙O的内接四边形，若∠A＝70°，则∠C的度数是（ ）
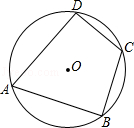A、100° B、110° C、120° D、130°3. 在同一平面内，⊙O的半径为5cm，点A到圆心O的距离OA＝3cm，则点A与圆O的位置关系为（ ）A、点A在圆内 B、点A在圆上 C、点A在圆外 D、无法确定4. 关于反比例函数y＝﹣ ，下列说法正确的是（ ）A、图象过（1，2）点 B、图象在第一、三象限 C、当x＞0时，y随x的增大而减小 D、当x＜0时，y随x的增大而增大5. 对于二次函数y＝﹣x2+2x﹣4，下列说法正确的是（ ）A、图象开口向上 B、对称轴是x＝2 C、当x＞1时，y随x的增大而减小 D、图象与x轴有两个交点6. 已知二次函数y＝ax2+bx+c的图象如图所示，那么下列判断不正确的是（ ）
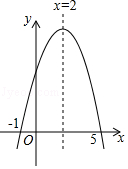A、b2﹣4ac＞0 B、a﹣b+c＞0 C、b＝﹣4a D、关于x的方程ax2+bx+c＝0的根是x1＝﹣1，x2＝57. 在平面直角坐标系中，将A（﹣1，5）绕原点逆时针旋转90°得到A′，则点A′的坐标是（ ）A、（﹣1，5） B、（5，﹣1） C、（﹣1，﹣5） D、（﹣5，﹣1）8. 如图，幼儿园计划用30m的围栏靠墙围成一个面积为100m2的矩形小花园（墙长为15m），则与墙垂直的边x为（ ）
A、10m或5m B、5m或8m C、10m D、5m9. 如图，在平面直角坐标系中，点P(1，4)、Q(m，n)在函数y＝ (k＞0)的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C，D，QD交PA于点E，随着m的增大，四边形ACQE的面积（ ）
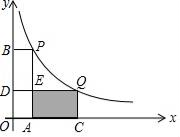A、增大 B、减小 C、先减小后增大 D、先增大后减小二、填空题（共24分）
-
10. 已知关于x的方程x2+3x+a＝0有一个根为﹣2，则另一个根为 ．11. 抛物线y＝﹣x2+1向右平移2个单位长度，再向下平移3个长度单位得到的抛物线解析式是 ．12. 如图所示，△ABC中，∠BAC＝33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为 ．
13. 如图是一个可以自由转动的转盘，如表是一次活动中的一组统计数据：转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”的次数m
68
111
136
345
546
701
转动转盘一次，落在“铅笔”的概率约是（结果保留小数点后一位）．
14. 若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为 ．15. 如图，在平面内2条直线相交最多形成1个交点，3条直线相交最多形成3个交点，4条直线相交最多形成6个交点，现有10条直线相交最多形成个交点．
三、解答题（一）（共18分）
-
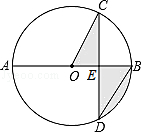
16. 解方程：3x2﹣2x﹣3＝0．17. 如图，AB是⊙O的直径，弦CD⊥AB于E，∠CDB＝30°，CD＝ ，求阴影部分的面积．
18. 如图如示，王强在一次高尔夫球的练习中，在O点处击球，球的飞行路线满足抛物线 ，其中y（米）是球的飞行高度，x（米）是球飞出的水平距离，球落地时离洞的水平距离为2米．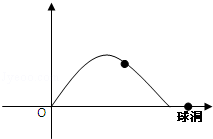
(1)、求此次击球中球飞行的最大水平距离；(2)、若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球的飞行路线应满足怎样的抛物线？求出其解析式．四、解答题（二）（共21分）
-
19. 某钢铁厂计划今年第一季度一月份的总产量为500t，三月份的总产量为720t，若平均每月的增长率相同．(1)、第一季度平均每月的增长率；(2)、如果第二季度平均每月的增长率保持与第一季度平均每月的增长率相同，请你估计该厂今年5月份总产量能否突破1000t？20. 如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，∠EAD＝45°，将△ADC绕点A顺时针旋转90°，得到△AFB，连接EF．
(1)、求证：EF＝ED；(2)、若AB＝2 ，CD＝1，求FE的长．21. 小明、小刚和小红各自打算随机选择元旦的上午或下午去红花湖景区游玩画树状图解答下列问题：(1)、小明和小刚都在元旦上午去游玩的概率为；(2)、求他们三人在同一个半天去游玩的概率．五、解答题（三）（共27分）
-
22. 如图，直线y＝﹣x+1与反比例函数y＝ 的图象相交于点A、B，过点A作AC⊥x轴，垂足为点C（﹣2，0），连接AC、BC．
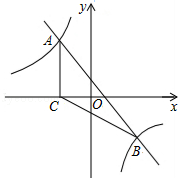(1)、求反比例函数的解析式；(2)、求S△ABC；(3)、利用函数图象直接写出关于x的不等式﹣x+1＜ 的解集．23. 如图，在△ABC中，AB＝AC，∠BAC＝54°，以AB为直径的⊙O分别交AC、BC于点D、E，过点B作直线BF，交AC的延长线于点F．
(1)、求证：BE＝CE；(2)、若AB＝6，求弧DE的长；(3)、当∠F的度数是多少时，BF与⊙O相切，证明你的结论．24. 如图，△ABC中，∠ACB＝90°，AC＝CB＝2，以BC为边向外作正方形BCDE，动点M从A点出发，以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动（M不与A、D重合）；过点M作直线l⊥AD，l与路线A→B→D相交于N，设运动时间为t秒：
(1)、填空：当点M在AC上时，BN＝（用含t的代数式表示）；(2)、当点M在CD上时（含点C），是否存在点M，使△DEN为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由；(3)、过点N作NF⊥ED，垂足为F，矩形MDFN与△ABD重叠部分的面积为S，求S的最大值．