广东省广州市天河区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-04-16 类型：期末考试
一、选择题（共30分）
-
1. 下列美丽的图案中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列各组线段长为边，不能组成三角形的是（ ）A、8cm，7cm，13cm B、6cm，6cm，12cm C、5cm，5cm，2cm D、10cm，15cm，17cm3. 点（3，﹣2）关于x轴的对称点坐标是（ ）A、（3，2） B、（﹣3，﹣2） C、（﹣3，2） D、（3，﹣2）4. 使分式有意义的x的取值范围是（ ）A、x＞﹣2 B、x＜2 C、x≠2 D、x≠﹣25. 下列运算中正确的是（ ）A、 B、（a﹣b）（﹣a﹣b）＝a2﹣b2 C、2a2•a3＝2a6 D、（﹣a）10÷（﹣a）4＝a66. 若一个多边形的内角和是1080°，则此多边形的边数是（ ）A、十二 B、十 C、八 D、十四7. 等腰三角形的两边长分别为3cm和7cm，则周长为（ ）A、13cm B、17cm C、13cm或17cm D、11cm或17cm8. 如图，在△ABC中，∠C＝90°，AB的垂直平分线交AB于D，交BC于E，连接AE，若CE＝5，AC＝12，且△ACE的周长为30，则BE的长是（ ）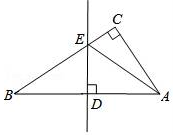
A、5 B、10 C、12 D、139. 已知a＝2﹣2 ， b＝（π﹣2）0 ， c＝（﹣1）3 ， 则a，b，c的大小关系为（ ）A、c＜b＜a B、b＜a＜c C、c＜a＜b D、a＜c＜b10. 如图，已知AB＝AC，AF＝AE，∠EAF＝∠BAC，点C、D、E、F共线．则下列结论，其中正确的是（ ）
①△AFB≌△AEC；②BF＝CE；③∠BFC＝∠EAF；④AB＝BC．
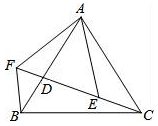A、①②③ B、①②④ C、①② D、①②③④二、填空题（共18分）
-
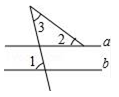
11. 已知xm＝8，xn＝2，则xm﹣n＝ ．12. 若分式 的值为0，则x＝ ．13. 如图，直线a∥b，∠1＝70°，∠2＝35°，则∠3的度数是 ．
14. 如图，已知∠ABC＝∠DCB，添加一个条件，使△ABC≌△DCB，你添加的条件是 ． （注：只需写出一个条件即可）
15. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是∠BAC的角平分线，DE⊥AB，垂足为E，DE＝1，则BC＝ ．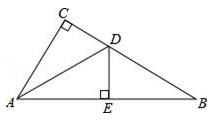
16. 若（x+p）与（x+5）的乘积中不含x的一次项，则p＝ ．三、解答题（共102分）
-
17.(1)、分解因式：3x3﹣27x(2)、18. 先化简，再求值：（﹣x﹣2y）（x﹣2y）+（2x3﹣4x2y）÷2x，其中x＝﹣2，y＝1．19. 如图1，方格图中每个小正方形的边长为1，点A、B、C都是格点．
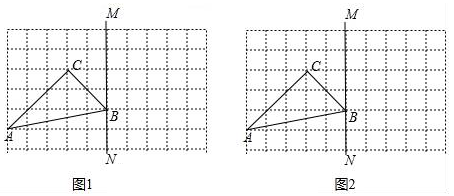(1)、画出△ABC关于直线MN对称的△A1B1C1；(2)、直接写出AA1的长度；(3)、如图2，A、C是直线MN同侧固定的点，D是直线MN上的一个动点，在直线MN上画出点D，使AD+DC最小．（保留作图痕迹）20. 如图，已知点E、F在AB上，AD＝BC，∠A＝∠B，∠C＝∠D．求证：AE＝BF．
21. 如图所示，在△ABC中，D是BC边上一点∠1＝∠2，∠3＝∠4，∠BAC＝69°，求∠DAC的度数．
22. 某校为创建“书香校园”，购置了一批图书，已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普类图书的数量与购买文学类图书的数量相等．求科普类图书平均每本的价格．23. 已知A＝ ﹣ ，B＝（x+2）（x+4）+1．(1)、化简A，并对B进行因式分解；(2)、当B＝0时，求A的值．24. 如图，等腰直角三角形ABD中，∠A＝90°，AB＝AD＝2，作△ABD关于直线BD对称的△CBD，已知点F为线段AB上一点，且AF＝m，连接CF，作∠FCE＝90°，CE交AD的延长线于点E．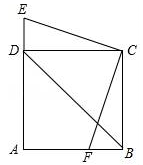
(1)、求证：△BCF≌△DCE；(2)、若AE＝n，且mn＝3，求m2+n2的值．25. △ABC中，∠BAC＞90°，∠ACB＝∠ABC＝α，点D为BC边上任意一点，点E在AD延长线上，且BC＝BE．
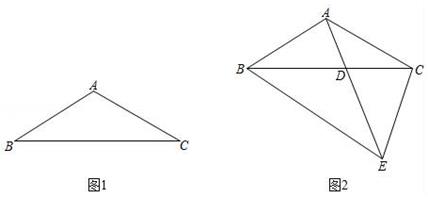(1)、当α＝30°，点D恰好为BC中点时，补全图1，求∠BEA的度数；(2)、如图2，若∠BAE＝2α，此时恰好DB＝DE，连接CE，求证：△ABE≌△CEB．