广东省佛山市顺德区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-04-16 类型:期末考试
一、选择题(共30分)
-
1. 正数9的平方根是( )A、3 B、±3 C、 D、±2. 能作为直角三角形的三边长的数据是( )A、3,4,6 B、5,12,14 C、1, ,2 D、 , ,23. 一次函数y=2x+b(其中b<0)的图象可能是( )A、
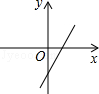 B、
B、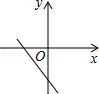 C、
C、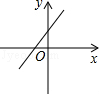 D、
D、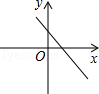 4. 平面直角坐标系中,点P(﹣2,1)关于y轴对称点P的坐标是( )A、(﹣2,1) B、(2,﹣1) C、(﹣2,﹣1) D、(2,1)5. 下列4组数值,哪个是二元一次方程2x+3y=5的解。( )
4. 平面直角坐标系中,点P(﹣2,1)关于y轴对称点P的坐标是( )A、(﹣2,1) B、(2,﹣1) C、(﹣2,﹣1) D、(2,1)5. 下列4组数值,哪个是二元一次方程2x+3y=5的解。( )
A、 B、 C、 D、6. 能判定直线a∥b的条件是( )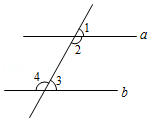 A、∠1=58°,∠3=59° B、∠2=118°,∠3=59° C、∠2=118°,∠4=119° D、∠1=61°,∠4=119°7. 某地区汉字听写大赛中,10名学生得分情况如下表:
A、∠1=58°,∠3=59° B、∠2=118°,∠3=59° C、∠2=118°,∠4=119° D、∠1=61°,∠4=119°7. 某地区汉字听写大赛中,10名学生得分情况如下表:分数
50
85
90
95
人数
3
4
2
1
那么这10名学生所得分数的中位数和众数分别是( )
A、85和85 B、85.5和85 C、85和82.5 D、85.5和808. 已知,如图,OA=OB,那么数轴上的点A所表示的数是( )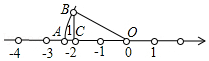 A、 B、 C、﹣ D、﹣9. 如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A、 B、 C、﹣ D、﹣9. 如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )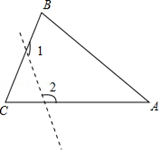 A、282° B、180° C、360° D、258°10. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )
A、282° B、180° C、360° D、258°10. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )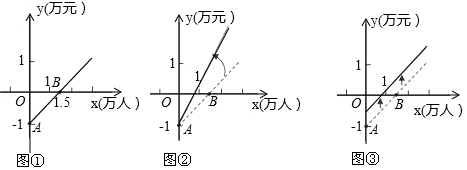 A、图①中点A的实际意义是公交公司运营后亏损1万元 B、图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡 C、图②能反映公交公司意见 D、图③能反映乘客意见
A、图①中点A的实际意义是公交公司运营后亏损1万元 B、图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡 C、图②能反映公交公司意见 D、图③能反映乘客意见二、填空题(共24分)
-
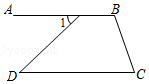
11. 比较大小: .(填“>、<、或=”)12. 数据4,5,6的方差是 .13. 如图,若∠1=∠D,∠C=72°,则∠B= .
 14. 如图,等边三角形ABC的顶点在坐标轴上,边长为4,则点A的坐标是 .
14. 如图,等边三角形ABC的顶点在坐标轴上,边长为4,则点A的坐标是 .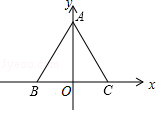 15. 在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.一根弹簧不挂物体时长15cm;当所挂物体的质量为5kg时,弹簧长20cm.所挂物体质量为8kg时弹簧的长度是cm.16. 某个正数的平方根是x与y,3x﹣y的立方根是2,则这个正数是 .
15. 在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.一根弹簧不挂物体时长15cm;当所挂物体的质量为5kg时,弹簧长20cm.所挂物体质量为8kg时弹簧的长度是cm.16. 某个正数的平方根是x与y,3x﹣y的立方根是2,则这个正数是 .三、解答题(一)(共18分)
-
17. 计算: +2 × ﹣ .18. 已知一次函数y=﹣x+3.
 (1)、当x=﹣3时,函数值是多少?(2)、画出函数图象.19. 某校有两种类型的学生宿舍30间,大的宿舍每间可住8人,小的每间可住5人,该校198个住宿生恰好住满这30间宿舍.大小宿舍各有多少间?
(1)、当x=﹣3时,函数值是多少?(2)、画出函数图象.19. 某校有两种类型的学生宿舍30间,大的宿舍每间可住8人,小的每间可住5人,该校198个住宿生恰好住满这30间宿舍.大小宿舍各有多少间?四、解答题(二)(共21分)
-
20. 国家规定“中小学生每天在校体育活动时间不低于1小时(h)”,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h.
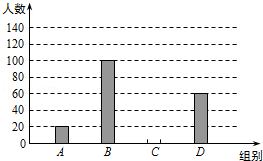
请根据上述信息解答下列问题
(1)、补全条形统计图;(2)、某市约有25000名初中学生,请你结合以上数据进行分析:①估计达到国家规定体育活动时间的人数是多少?
②如果要估算本市初中生每天在校体育活动时间是多少,你认为选择众数、中位数和平均数三个量中的哪个更合适?
21. 如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.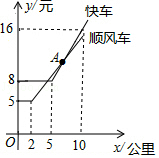 (1)、由图象写出乘车里程为5千米时选择(“顺风车”或“快车”)更便宜;(2)、当x>5时,顺风车的函数是y= x+ ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.22. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
(1)、由图象写出乘车里程为5千米时选择(“顺风车”或“快车”)更便宜;(2)、当x>5时,顺风车的函数是y= x+ ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.22. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?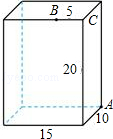
五、解答题(三)(共27分)
-
23. 已知点A(0,4)、C(﹣2,0)在直线l:y=kx+b上,l和函数y=﹣4x+a的图象交于点B。
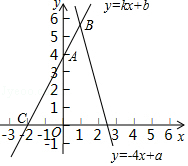 (1)、求直线l的表达式;(2)、若点B的横坐标是1,求关于x、y的方程组 的解及a的值.(3)、若点A关于x轴的对称点为P,求△PBC的面积.24. 如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)、求直线l的表达式;(2)、若点B的横坐标是1,求关于x、y的方程组 的解及a的值.(3)、若点A关于x轴的对称点为P,求△PBC的面积.24. 如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.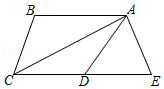 (1)、求证:AB∥CD;(2)、若AE=5,AC=12,求线段CE的长;(3)、在(2)的条件下,若线段CD上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.25. 如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.
(1)、求证:AB∥CD;(2)、若AE=5,AC=12,求线段CE的长;(3)、在(2)的条件下,若线段CD上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.25. 如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.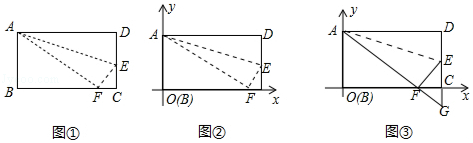 (1)、求CE的长;(2)、建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;(3)、如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.
(1)、求CE的长;(2)、建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;(3)、如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.