2016-2017学年河南省信阳市新县高三下学期开学数学试卷（理科）

试卷更新日期：2017-05-09 类型：开学考试

进入出卷网下载

一、选择题：

1. 已知集合A={x|x²≥16}，B={m}，若A∪B=A，则实数m的取值范围是（）

A、（﹣∞，﹣4） B、[4，+∞） C、[﹣4，4] D、（﹣∞，﹣4]∪[4，+∞）

查看试题解析
2. 已知复数Z的共轭复数 $\bar{Z}$ = $\frac{1 - i}{1 + 2 i}$ ，则复数Z的虚部是（）

A、 $\frac{3}{5}$ B、 $\frac{3}{5}$ i C、﹣ $\frac{3}{5}$ D、﹣ $\frac{3}{5}$ i

查看试题解析
3. 若 $f (x) = {\begin{matrix} {(\frac{1}{3})}^{x} ， x \leq 0 \\ \log_{3} x ， x > 0 \end{matrix}$ ，则 $f (f (\frac{1}{9}))$ =（）

A、﹣2 B、﹣3 C、9 D、 $\frac{1}{9}$

查看试题解析
4. 若{a_n}为等差数列，S_n是其前n项和，且S₁₁= $\frac{22 π}{3}$ ，{b_n}为等比数列，b₅•b₇= $\frac{π^{2}}{4}$ ，则tan（a₆+b₆）的值为（）

A、 $\sqrt{3}$ B、 $\pm \sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\pm \frac{\sqrt{3}}{3}$

查看试题解析
5. 执行如图所示的程序框图，则输出的结果是（）

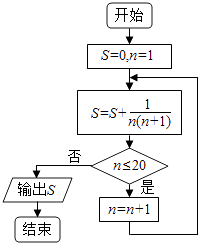A、 $\frac{19}{20}$ B、 $\frac{20}{21}$ C、 $\frac{21}{22}$ D、 $\frac{22}{23}$

查看试题解析
6. 已知点P是抛物线x²=4y上的动点，点P在x轴上的射影是Q，点A（8，7），则|PA|+|PQ|的最小值为（）

A、7 B、8 C、9 D、10

查看试题解析
7. 已知 ${\begin{matrix} x - y + 2 \geq 0 \\ 7 x - y - 7 \leq 0 \\ x \geq 0 ， y \geq 0 \end{matrix}$ 表示的平面区域为D，若∀（x，y）∈D，2x+y≤a为真命题，则实数a的取值范围是（）

A、[5，+∞） B、[2，+∞） C、[1，+∞） D、[0，+∞）

查看试题解析
8. 一个空间几何体的三视图如右图所示，其中主视图和侧视图都是半径为1的圆，且这个几何体是球体的一部分，则这个几何体的表面积为（）

A、3π B、4π C、6π D、8π

查看试题解析
9. 已知双曲线M： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a＞0，b＞0）的一个焦点到一条渐近线的距离为 $\frac{\sqrt{2}}{3} c$ （c为双曲线的半焦距长），则双曲线的离心率e为（）

A、 $\frac{\sqrt{7}}{3}$ B、 $\frac{3 \sqrt{7}}{2}$ C、 $\frac{3 \sqrt{7}}{7}$ D、 $3 \sqrt{7}$

查看试题解析
10. 将三颗骰子各掷一次，记事件A=“三个点数都不同”，B=“至少出现一个6点”，则条件概率P（A|B），P（B|A）分别是（）

A、 $\frac{60}{91}$ ， $\frac{1}{2}$ B、 $\frac{1}{2}$ ， $\frac{60}{91}$ C、 $\frac{5}{18}$ ， $\frac{60}{91}$ D、 $\frac{91}{216}$ ， $\frac{1}{2}$

查看试题解析
11. 设x，y∈R，则（3﹣4y﹣cosx）²+（4+3y+sinx）²的最小值为（　　）

A、4 B、5 C、16 D、25

查看试题解析
12. 当|a|≤1，|x|≤1时，关于x的不等式|x²﹣ax﹣a²|≤m恒成立，则实数m的取值范围是（　　）

A、[ $\frac{3}{4}$ ， +∞） B、[ $\frac{5}{4}$ ， +∞） C、[ $\frac{3}{2}$ ， +∞） D、[ $\frac{5}{2}$ ， +∞）

查看试题解析

二、填空题：

13. 设命题P：∃x₀∈（0，+∞）， $3^{x_{0}}$ ＜ $x_{0}^{3}$ ，则命题￢p为．

查看试题解析
14. $a = \int \begin{array}{l} π \\ 0 \end{array} (\sin x + \cos x) d x ，则二项式 {(a \sqrt{x} - \frac{1}{\sqrt{x}})}^{6}$ 展开式中含x²项的系数是．

查看试题解析
15. 已知点A在椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ 上，点P满足 $\vec{A P} = (λ - 1) \vec{O A} (λ \in R)$ ，且 $\vec{O A} \cdot \vec{O P} = 72$ ，则线段OP在x轴上的投影长度的最大值为．

查看试题解析
16. 已知函数 $f (x) = {\begin{matrix} | \ln (- x) | ， x < 0 \\ x^{2} - 4 x + 3 ， x \geq 0 \end{matrix}$ ，若H（x）=f²（x）﹣2bf（x）+3有8个不同的零点，则实数b的取值范围为．

查看试题解析

三、解答题：

17.
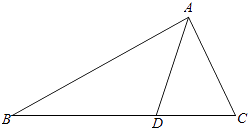
如图，在△ABC中，点D在BC边上，∠CAD= $\frac{π}{4}$ ，AC= $\frac{7}{2}$ ，cos∠ADB=﹣ $\frac{\sqrt{2}}{10}$ ．
（Ⅰ）求sin∠C的值；
（Ⅱ）若BD=5，求△ABD的面积．

查看试题解析
18. 心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学（男30女20），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答．选题情况如右表：（单位：人）
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
附表及公式
P（k²≥k）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + c) (a + c) (b + d)}$ ．

(1)、能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？

(2)、经过多次测试后，甲每次解答一道几何题所用的时间在5～7分钟，乙每次解答一道几何题所用的时间在6～8分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．

(3)、现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、乙两女生被抽到的人数为 X，求 X的分布列及数学期望 EX．

查看试题解析
19. 已知S_n为数列{a_n}的前n项和，且有a₁=1，S_n+1=a_n₊₁（n∈N^*）．

(1)、求数列{a_n}的通项a_n；

(2)、若b_n= $\frac{n}{4 a_{n}}$ ，求数列{b_n}的前n项和T_n；

(3)、设c_k= $\frac{k + 2}{S_{k} (T_{k} + k + 1)}$ ，{c_k}的前n项和为A_n ，是否存在最小正整数m，使得不等式A_n＜m对任意正整数n恒成立？若存在，求出m的值；若不存在，说明理由．

查看试题解析
20. 已知椭圆 $W ： \frac{b^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，其左顶点A在圆O：x²+y²=16上．
（Ⅰ）求椭圆W的方程；
（Ⅱ）若点P为椭圆W上不同于点A的点，直线AP与圆O的另一个交点为Q．是否存在点P，使得 $\frac{| P Q |}{| A P |} = 3$ ？若存在，求出点P的坐标；若不存在，说明理由．

查看试题解析
21. 已知函数f（x）=ln（1+x²）+ax．（a≤0）

(1)、若f（x）在x=0处取得极值，求a的值；

(2)、讨论f（x）的单调性；

(3)、证明：（1+ $\frac{1}{9}$ ）（1+ $\frac{1}{81}$ ）…（1+ $\frac{1}{3^{2 n}}$ ）＜ $\sqrt{e}$ （n∈N^* ， e为自然对数的底数）．

查看试题解析
22. 在平面直角坐标系xOy中，圆C的参数方程为 ${\begin{matrix} x = - 5 + \sqrt{2} \cos t \\ y = 3 + \sqrt{2} \sin t \end{matrix}$ ，（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为 $ρ \cos (θ + \frac{π}{4}) = - \sqrt{2}$ ，A，B两点的极坐标分别为 $A (2 ， \frac{π}{2}) ， B (2 ， π)$ ．

(1)、求圆C的普通方程和直线l的直角坐标方程；

(2)、点P是圆C上任一点，求△PAB面积的最小值．

查看试题解析
23. 已知函数f（x）=|x﹣2|．

(1)、解不等式：f（x+1）+f（x+2）＜4；

(2)、已知a＞2，求证：∀x∈R，f（ax）+af（x）＞2恒成立．

查看试题解析

	几何题	代数题	总计
男同学	22	8	30
女同学	8	12	20
总计	30	20	50

P（k²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828