2017年天津市河西区中考数学模拟试卷
试卷更新日期:2017-05-09 类型:中考模拟
一、选择题
-
1. 2sin45°的值是( )A、 B、 C、 D、32.
下列图案中,可以看作是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 已知一个反比例函数的图象经过点A(3,﹣4),那么不在这个函数图象上的点是( )A、(﹣3,﹣4) B、(﹣3,4) C、(2,﹣6) D、( ,﹣12 )4. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )
A、1个 B、2个 C、3个 D、4个3. 已知一个反比例函数的图象经过点A(3,﹣4),那么不在这个函数图象上的点是( )A、(﹣3,﹣4) B、(﹣3,4) C、(2,﹣6) D、( ,﹣12 )4. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )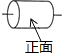 A、
A、 B、
B、 C、
C、 D、
D、 5. 估计 的值在( )A、2到3之间 B、3到4之间 C、2到3之间或﹣3到﹣2之间 D、3到4之间或﹣4到﹣3之间6. 在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )A、不断变大 B、不断减小 C、不变 D、不能确定7. 如图是由几个相同的小立方块组成的三视图,小立方块的个数是( )
5. 估计 的值在( )A、2到3之间 B、3到4之间 C、2到3之间或﹣3到﹣2之间 D、3到4之间或﹣4到﹣3之间6. 在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )A、不断变大 B、不断减小 C、不变 D、不能确定7. 如图是由几个相同的小立方块组成的三视图,小立方块的个数是( ) A、3个 B、4个 C、5个 D、6个8. 一次函数y=2x﹣1与反比例函数y=﹣ 的图像的交点的情况为( )A、只有一个交点 B、有两个交点 C、没有交点 D、不能确定9. 已知圆的半径为R,这个圆的内接正六边形的面积为( )A、 R2 B、 R2 C、6R2 D、1.5R210. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)11. 如图,直线l1过原点,直线l2解析式为y=﹣ x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
A、3个 B、4个 C、5个 D、6个8. 一次函数y=2x﹣1与反比例函数y=﹣ 的图像的交点的情况为( )A、只有一个交点 B、有两个交点 C、没有交点 D、不能确定9. 已知圆的半径为R,这个圆的内接正六边形的面积为( )A、 R2 B、 R2 C、6R2 D、1.5R210. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)11. 如图,直线l1过原点,直线l2解析式为y=﹣ x+2,且直线l1和l2互相垂直,那么直线l1解析式为( ) A、y= x B、y= x C、y= x D、y= x12. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+
A、y= x B、y= x C、y= x D、y= x12. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+二、填空题
-
13. 写出一个反比例函数,使它的图像经过第二、四象限,它是 .14. 如图,在△ABC中,DE∥BC,且AD=2,DB=3,则 = .
 15. 已知反比例函数 的图像上有两点A(x1 , y1)、B(x2 , y2),当x1<0<x2时,有y1<y2 , 则m的取值范围是 .16. 如图,是一个物体的展开图(单位:cm),那么这个物体的体积为 .
15. 已知反比例函数 的图像上有两点A(x1 , y1)、B(x2 , y2),当x1<0<x2时,有y1<y2 , 则m的取值范围是 .16. 如图,是一个物体的展开图(单位:cm),那么这个物体的体积为 .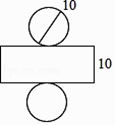 17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 cm,且tan∠EFC= ,则矩形ABCD的周长是 .
17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 cm,且tan∠EFC= ,则矩形ABCD的周长是 . 18. 如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为 .
18. 如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为 .
三、解答题
-
19. 如图,在△ABC中,∠C=90°,∠B=37°,若BC=3.求:AC、AB的长(结果保留小数点后一位).参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.
 20. 如图△OPQ是边长为 的等边三角形,若反比例函数y= 的图像过点P.
20. 如图△OPQ是边长为 的等边三角形,若反比例函数y= 的图像过点P.(Ⅰ)求点P的坐标和k的值;
(Ⅱ)若在这个反比例函数的图象上有两个点(x1 , y1)(x2 , y2),且x1<x2<0,请比较y1与y2的大小.
 21.
21.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
 22. 某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:(1)、油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?(2)、如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?23. 如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5.
22. 某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:(1)、油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?(2)、如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?23. 如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5. (1)、如图(1),若点P是 的中点,求PA的长;(2)、如图(2),若点P是 的中点,求PA的长.24. 如图①,将边长为2的正方形OABC如图①放置,O为原点.
(1)、如图(1),若点P是 的中点,求PA的长;(2)、如图(2),若点P是 的中点,求PA的长.24. 如图①,将边长为2的正方形OABC如图①放置,O为原点.(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
 25.
25.如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
 (1)、求抛物线的解析式;(2)、点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
(1)、求抛物线的解析式;(2)、点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.