2017年天津市河北区中考数学模拟试卷
试卷更新日期：2017-05-09 类型：中考模拟
一、选择题
-
1. 下列图形中，不是中心对称图形的是（ ）A、平行四边形 B、圆 C、正八边形 D、等边三角形2. 由六个相同的立方体拼成的几何体如图所示，则它的主视图是（ ）
A、
B、
C、
D、
3. 如图中主三视图对应的三棱柱是（ ）
A、
B、
C、
D、
4. 已知x1 ， x2是一元二次方程x2﹣6x﹣15﹣0的两个根，则x1+x2等于（ ）A、﹣6 B、6 C、﹣15 D、155. 二次函数y=x2﹣4x﹣4的顶点坐标为（ ）A、（2，﹣8） B、（2，8） C、（﹣2，8） D、（﹣2，﹣8）6. 如图，在⊙O中， = ，∠AOB=40°，则∠ADC的度数是（ ）
A、15° B、20° C、30° D、40°7. 一副完整的扑克牌，去掉大小王，将剩余的52张混合后从中随机抽取一张，则抽出A的概率是（ ）A、 B、 C、 D、8. 对于函数y=﹣ ，当x＜0时，函数图象位于（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图，在4×4的正方形方格网中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）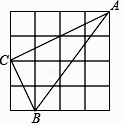
A、 B、 C、 D、210. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA=1：25，则S△BDE与S△CDE的比是（ ）
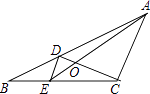A、1：3 B、1：4 C、1：5 D、1：2511. 已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（ ）A、 B、 C、 D、212. 二次函数y=ax2+bx+c（a≠0）和正比例函数y= x的图像如图所示，则方程ax2+（b﹣ ）x+c=0（a≠0）的两根之和（ ）
A、大于0 B、等于0 C、小于0 D、不能确定二、填空题
-
13. 计算cos60°= ．14. 两个实数的和为4，积为﹣7，则这两个实数为 ．15. 已知直角三角形的两直角边分别为8和15，则这个三角形的内切圆的直径为 ．16. 若二次函数y=x2﹣x﹣2的函数值小于0，则x的取值范围是 ．17. 有3个正方形如图所示放置，阴影部分的面积依次记为S1 ， S2 ， 则S1：S2= ．
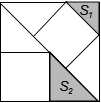18. 如图，MN是⊙O的直径，MN=2，点A在⊙O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为 ．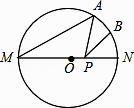
三、解答题
-
19. 如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求△ABC的周长．
20. 如图，直线y= x+2与双曲线y= 相交于点A（m，3），与x轴交于点C．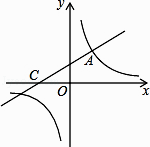
(1)、求双曲线解析式；(2)、点P在x轴上，如果△ACP的面积为3，求点P的坐标．21. 如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4，如图2，正方形ABCD顶点处各有一个圈，跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．例如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D，若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B，…设游戏者从圈A起跳．
(1)、若随机掷一次骰子，求落回到圈A的概率P1；(2)、若随机掷两次骰子，用列表法或树状图法求出最后落回到圈A的概率P．22. 如图，在矩形ABCD中，点O在对角线AB上，以OA的长为半径的圆O与AD交于点E，且∠ACB=∠DCE，求证：CE是⊙O的切线．
23. 如图，在平面直角坐标系中，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A（1，0）、B（3，0）两点，与y轴交于点C，其顶点为D．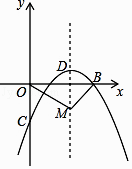
(1)、求抛物线的解析式；(2)、一动点M从点D出发，以每秒1个单位的速度沿抛物线的对称轴向下运动，连OM，BM，设运动时间为t秒（t=0），在点M的运动过程中，当∠OMB=90°时，求t的值．24. 如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．
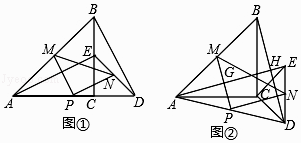(1)、求证：△PMN为等腰直角三角形；(2)、现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．