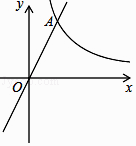2017年山东省聊城市阳谷县中考数学一模试卷
试卷更新日期:2017-05-09 类型:中考模拟
一、选择题
-
1. 义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )A、3.5×108 B、3.5×109 C、35×108 D、0.35×1092.
下列图形中是中心对称图形的有( )个.
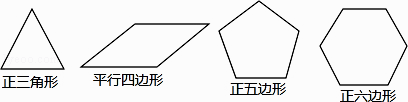 A、1 B、2 C、3 D、43. 下列各运算中,计算正确的是( )A、(﹣3ab2)2=9a2b4 B、2a+3b=5ab C、 =±3 D、(a﹣b)2=a2﹣b24. 如图,将一只青花碗放在水平桌面上,它的左视图是( )
A、1 B、2 C、3 D、43. 下列各运算中,计算正确的是( )A、(﹣3ab2)2=9a2b4 B、2a+3b=5ab C、 =±3 D、(a﹣b)2=a2﹣b24. 如图,将一只青花碗放在水平桌面上,它的左视图是( )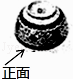 A、
A、 B、
B、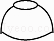 C、
C、 D、
D、 5. 为了了解2016年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )A、2016年我县九年级学生是总体 B、每一名九年级学生是个体 C、200名九年级学生是总体的一个样本 D、样本容量是2006. 已知a>b,下列关系式中一定正确的是( )A、a2<b2 B、2a<2b C、a+2<b+2 D、﹣a<﹣b7. 已知等腰三角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )A、相离 B、相切 C、相交 D、不能确定8. 解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )A、(x﹣4)2=21 B、(x﹣4)2=11 C、(x+4)2=21 D、(x+4)2=119. 如图,直线y1= x+2与双曲线y2= 交于A(2,m)、B(﹣6,n)两点,则当y1<y2时,x的取值范围是( )
5. 为了了解2016年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )A、2016年我县九年级学生是总体 B、每一名九年级学生是个体 C、200名九年级学生是总体的一个样本 D、样本容量是2006. 已知a>b,下列关系式中一定正确的是( )A、a2<b2 B、2a<2b C、a+2<b+2 D、﹣a<﹣b7. 已知等腰三角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )A、相离 B、相切 C、相交 D、不能确定8. 解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )A、(x﹣4)2=21 B、(x﹣4)2=11 C、(x+4)2=21 D、(x+4)2=119. 如图,直线y1= x+2与双曲线y2= 交于A(2,m)、B(﹣6,n)两点,则当y1<y2时,x的取值范围是( )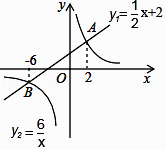 A、x<﹣6或x>2 B、﹣6<x<0或x>2 C、x<﹣6或0<x<2 D、﹣6<x<210. 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
A、x<﹣6或x>2 B、﹣6<x<0或x>2 C、x<﹣6或0<x<2 D、﹣6<x<210. 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )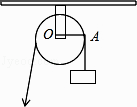 A、5πcm B、3πcm C、2πcm D、πcm11. 已知抛物线y=ax2+bx+c的图像如图所示,则下列结论:
A、5πcm B、3πcm C、2πcm D、πcm11. 已知抛物线y=ax2+bx+c的图像如图所示,则下列结论:①abc>0;②a+b+c=2;③b>1;④a< .
其中正确的结论是( )
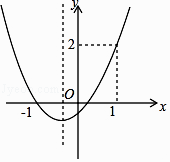 A、①② B、②③ C、③④ D、②④12. 如图,在平面内直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )
A、①② B、②③ C、③④ D、②④12. 如图,在平面内直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )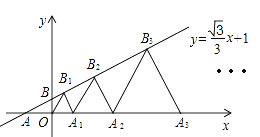
A、2n B、(2n+1) C、(2n﹣1﹣1) D、(2n﹣1)二、填空题
-
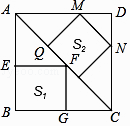
13. 如果线段a、b、c、d满足 = = ,那么 = .14. 某中学规定学生的学期体育总评成绩满分为100分,其中平均成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育总评成绩为 .15. 已知,关于x的不等式组 的整数解共有两个,那么a的取值范围是 .16. 如图,大正方形ABCD中有2个小正方形,如果它们的面积分别是s1 , s2 , 那么s1s2 . (填>,<或=)
 17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是 cm2 .
17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是 cm2 .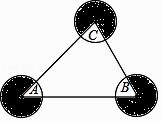
三、解答题
-
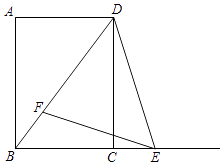
18. 化简求值与计算(1)、先化简,再求值:(1+ )÷ ,其中x= 1(2)、 .19. 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
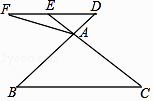 (1)、如果 = ,DE=6,求边BC的长;(2)、如果∠FAE=∠B,FA=6,FE=4,求DF的长.20. 某校九年级(1)、(2)两个班分别有一男一女4名学生报名参加全市中学生运动会.(1)、若从两班报名的学生中随之选1名,求所选的学生性别为女的概率;(2)、若从报名的4名学生中随机选2名,用列表或画树状图的方法求出这2名学生来自不同班的概率.21. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)、如果 = ,DE=6,求边BC的长;(2)、如果∠FAE=∠B,FA=6,FE=4,求DF的长.20. 某校九年级(1)、(2)两个班分别有一男一女4名学生报名参加全市中学生运动会.(1)、若从两班报名的学生中随之选1名,求所选的学生性别为女的概率;(2)、若从报名的4名学生中随机选2名,用列表或画树状图的方法求出这2名学生来自不同班的概率.21. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. (1)、求n的值;(2)、若F是DE的中点,判断四边形ACFD的形状,并说明理由.22. 抛物线L:y=ax2+bx+c与已知抛物线y= x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)(1)、求L的解析式;(2)、若L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C,求△ABC的面积.23. 如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)、求n的值;(2)、若F是DE的中点,判断四边形ACFD的形状,并说明理由.22. 抛物线L:y=ax2+bx+c与已知抛物线y= x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)(1)、求L的解析式;(2)、若L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C,求△ABC的面积.23. 如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.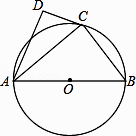 (1)、若BC=3,AB=5,求AC的值;(2)、若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
(1)、若BC=3,AB=5,求AC的值;(2)、若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.