2017年河南省平顶山市中考数学一模试卷

试卷更新日期：2017-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个实数中，无理数是（）

A、3.14 B、﹣π C、0 D、 $\sqrt{9}$

查看试题解析
2. 经统计，2016年除夕夜观看春晚直播的观众约达10.3亿人，用科学记数法表示10.3亿正确的是（）

A、1.03×10⁹ B、1.03×10¹⁰ C、10.3×10⁹ D、103×10⁸

查看试题解析
3. 下列几何体的主视图既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列调查中，适合普查的事件是（）

A、调查华为手机的使用寿命 B、调查市九年级学生的心理健康情况 C、调查你班学生打网络游戏的情况 D、调查中央电视台《中国舆论场》的节目收视率

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{2}$ =2 B、3+ $\sqrt{2}$ =3 $\sqrt{2}$ C、 $\sqrt{3}$ + $\sqrt{2}$ = $\sqrt{5}$ D、 $\sqrt{9}$ + $\sqrt{3}$ =3+ $\sqrt{3}$

查看试题解析
6. 下列不等式变形正确的是（）

A、由a＞b，得ac＞bc B、由a＞b，得a﹣2＜b﹣2 C、由﹣ $\frac{1}{2}$ ＞﹣1，得﹣ $\frac{a}{2}$ ＞﹣a D、由a＞b，得c﹣a＜c﹣b

查看试题解析
7. 如图，已知直线a∥b，∠1=46°．∠2=66°，则∠3等于（）

A、112° B、100° C、130° D、120°

查看试题解析
8. 不改变分式 $\frac{0.5 x - 1}{0.3 x + 2}$ 的值，如果把其分子和分母中的各项的系数都化为整数，那么所得的正确结果为（）

A、 $\frac{5 x - 1}{3 x + 2}$ B、 $\frac{5 x - 10}{3 x + 20}$ C、 $\frac{2 x - 1}{3 x + 2}$ D、 $\frac{x - 2}{3 x + 20}$

查看试题解析
9. 如图，一张长方形纸片的长AD=4，宽AB=1．点E在边AD上，点F在BC边上，将四边形 ABFE沿直线EF翻折后，点B落在边AD的中点G处，则EG等于（）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、 $\frac{5}{4}$ D、 $\frac{17}{8}$

查看试题解析
10.
如图所示，在平面直角坐标系中A（0，0），B（2，0），△AP₁B是等腰直角三角形，且∠P₁=90°，把△AP₁B绕点B顺时针旋转180°，得到△BP₂C；把△BP₂C绕点C顺时针旋转180°，得到△CP₃D，依此类推，则旋转第2016次后，得到的等腰直角三角形的直角顶点P₂₀₁₇的坐标为（）

A、（4030，1） B、（4029，﹣1） C、（4033，1） D、（4031，﹣1）

查看试题解析

二、填空题

11. （﹣2）^﹣²= ．

查看试题解析
12. 关于x的一元二次方程x²﹣3x+m=0有两个不相等的实数根，则m的取值范围为．

查看试题解析
13. 袋子里放着小颖刚买的花、白两种色彩的手套各1双（除颜色外其余都相同），小颖在看不见的情况下随机摸出两只手套，它们恰好同色的概率是．

查看试题解析
14. 如图，将半径为6的圆形纸片，分别沿AB、BC折叠，若弧AB和弧BC折后都经过圆心O，则阴影部分的面积是（结果保留π）

查看试题解析
15. 在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的四边形，AB∥CD，CD⊥BC于C，且AB、BC、CD边长分别为2，4，3，则原直角三角形纸片的斜边长是．

查看试题解析

三、解答题

16. 先化简，再求值：（x+y）²﹣2y（x+y），其中x= $\sqrt{2}$ ﹣1，y= $\sqrt{3}$ ．

查看试题解析
17. 某商场对一种新售的手机进行市场问卷调查，其中一个项目是让每个人按A（不喜欢）、B（一般）、C（不比较喜欢）、D（非常喜欢）四个等级对该手机进行评价，图①和图②是该商场采集数据后，绘制的两幅不完整的统计图，请你根据以上统计图提供的信息，回答下列问题：

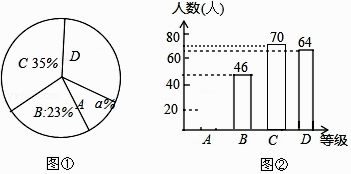(1)、本次调查的人数为多少人？A等级的人数是多少？请在图中补全条形统计图．

(2)、图①中，a等于多少？D等级所占的圆心角为多少度？

查看试题解析
18. 如图，在▱ABCD中，M，N分别是AD，BC的中点，∠AND=90°，连接CM交DN于点O．

(1)、求证：△ABN≌△CDM；

(2)、连接MN，求证四边形MNCD是菱形．

查看试题解析
19. 某商场将M品牌服装每套按进价的2倍进行销售，恰逢“春节”来临，为了促销，他将售价提高了50元再标价，打出了“大酬宾，八折优惠”的牌子，结果每套服装的利润是进价的 $\frac{2}{3}$ ，该老板到底给顾客优惠了吗？说出你的理由．

查看试题解析
20.
如图，一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船，该艘货船以每小时10海里的速度向正东航行，海警船立即以每小时14海里的速度追赶，到C处相遇，求海警船用多长时间追上了货船？

查看试题解析
21. 某单位举行“健康人生”徒步走活动，某人从起点体育村沿建设路到市生态园，再沿原路返回，设此人离开起点的路程s（千米）与走步时间t（小时）之间的函数关系如图所示，其中从起点到市生态园的平均速度是4千米/小时，用2小时，根据图像提供信息，解答下列问题．

(1)、求图中的a值．

(2)、若在距离起点5千米处有一个地点C，此人从第一次经过点C到第二次经过点C，所用时间为1.75小时．
①求AB所在直线的函数解析式；
②请你直接回答，此人走完全程所用的时间．

查看试题解析
22. 如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC的中点，DE⊥AB，垂足为E，交AC的延长线于点F．

(1)、求证：直线EF是⊙O的切线；

(2)、CF=5，cos∠A= $\frac{2}{5}$ ，求AE的长．

查看试题解析
23.
如图，抛物线y=ax²+bx+1与直线y=﹣ax+c相交于坐标轴上点A（﹣3，0），C（0，1）两点．

(1)、直线的表达式为；抛物线的表达式为．

(2)、D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交直线AC于点F，求线段DF长度的最大值，并求此时点D的坐标；

(3)、P为抛物线上一动点，且P在第四象限内，过点P作PN垂直x轴于点N，使得以P、A、N为顶点的三角形与△ACO相似，请直接写出点P的坐标．

查看试题解析