2016-2017学年江苏省苏州市高三上学期开学数学试卷

试卷更新日期：2017-05-09 类型：开学考试

进入出卷网下载

一、填空题：

1. 设集合A={﹣1，0，1}，B={x|x²+x≤0}，则A∩B= ．

查看试题解析
2. 命题“∃x＞1，使得x²≥2”的否定是．

查看试题解析
3. 已知i是虚数单位，复数z的共轭复数为 $\bar{z}$ ，若2z= $\bar{z}$ +2﹣3i，则z= ．

查看试题解析
4. 有4名学生A、B、C、D平均分乘两辆车，则“A，B两人恰好在同一辆车”的概率为．

查看试题解析
5. 函数y=e^x在x=0处的切线方程是．

查看试题解析
6. 如图是一个输出一列数的算法流程图，则这列数的第三项是．

查看试题解析
7. 定义在R上的奇函数f（x），当x＞0时，f（x）=2^x﹣x² ，则f（0）+f（﹣1）= ．

查看试题解析
8. 已知等差数列{a_n}的公差为d，若a₁ ， a₂ ， a₃ ， a₄ ， a₅的方差为8，则d的值为．

查看试题解析
9. 如图，在长方体ABCD﹣A₁B₁C₁D₁中，AB=AD=3cm，AA₁=2cm，则三棱锥A﹣B₁D₁D的体积为cm³ ．

查看试题解析
10. 已知α∈（0， $\frac{π}{2}$ ），β∈（ $\frac{π}{2}$ ，π），cosα= $\frac{1}{3}$ ，sin（α+β）=﹣ $\frac{3}{5}$ ，则cosβ= ．

查看试题解析
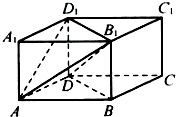11. 已知函数f（x）= ${\begin{cases} \frac{1}{x} ， x > 1 ， \\ x^{3} ， - 1 \leq x \leq 1 \end{cases}$ 若关于x的方程f（x）=k（x+1）有两个不同的实数根，则实数k的取值范围是．

查看试题解析
12. 圆心在抛物线 $y = \frac{1}{2} x^{2}$ （x＜0）上，并且与抛物线的准线及y轴都相切的圆的方程是．

查看试题解析
13. 设点P是△ABC内一点（不包括边界），且 $\vec{A P} = m \vec{A B} + n \vec{A C} ， m ， n \in R$ ，则（m﹣2）²+（n﹣2）²的取值范围是．

查看试题解析
14. 设a+b=2，b＞0，当 $\frac{1}{2 | a |}$ + $\frac{| a |}{b}$ 取得最小值时，a= ．

查看试题解析

二、解答题：

15. 在△ABC中，角A，B，C的对边分别为a，b，c．已知bcosC+ccosB=2acosA．

(1)、求角A的大小；

(2)、若 $\vec{A B}$ • $\vec{A C}$ = $\sqrt{3}$ ，求△ABC的面积．

查看试题解析
16. 如图，在四棱锥P﹣ABCD中，底面是正方形，侧面PAD⊥底面ABCD，且PA=PD= $\frac{\sqrt{2}}{2}$ AD，若E、F分别为PC、BD的中点．
（Ⅰ）求证：EF∥平面PAD；
（Ⅱ）求证：EF⊥平面PDC．

查看试题解析
17. 如图，在平面直角坐标系xOy中，椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁ ， F₂ ，点P（3，1）在椭圆上，△PF₁F₂的面积为2 $\sqrt{2}$ ．

(1)、①求椭圆C的标准方程；
②若∠F₁QF₂= $\frac{π}{3}$ ，求QF₁•QF₂的值．

(2)、直线y=x+k与椭圆C相交于A，B两点，若以AB为直径的圆经过坐标原点，求实数k的值．

查看试题解析
18. 如图，某城市小区有一个矩形休闲广场，AB=20米，广场的一角是半径为16米的扇形BCE绿化区域，为了使小区居民能够更好的在广场休闲放松，现决定在广场上安置两排休闲椅，其中一排是穿越广场的双人靠背直排椅MN（宽度不计），点M在线段AD上，并且与曲线CE相切；另一排为单人弧形椅沿曲线CN（宽度不计）摆放．已知双人靠背直排椅的造价每米为2a元，单人弧形椅的造价每米为a元，记锐角∠NBE=θ，总造价为W元．

(1)、试将W表示为θ的函数W（θ），并写出cosθ的取值范围；

(2)、如何选取点M的位置，能使总造价W最小．

查看试题解析
19. 在数列{a_n}中，已知a₁=2，a_n₊₁=3a_n+2n﹣1．

(1)、求证：数列{a_n+n}为等比数列；

(2)、记b_n=a_n+（1﹣λ）n，且数列{b_n}的前n项和为T_n ，若T₃为数列{T_n}中的最小项，求λ的取值范围．

查看试题解析
20. 已知函数f（x）=x﹣lnx，g（x）=x²﹣ax．

(1)、求函数f（x）在区间[t，t+1]（t＞0）上的最小值m（t）；

(2)、令h（x）=g（x）﹣f（x），A（x₁ ， h（x₁）），B（x₂ ， h（x₂））（x₁≠x₂）是函数h（x）图象上任意两点，且满足 $\frac{h (x_{1}) - h (x_{2})}{x_{1} - x_{2}}$ ＞1，求实数a的取值范围；

(3)、若∃x∈（0，1]，使f（x）≥ $\frac{a - g (x)}{x}$ 成立，求实数a的最大值．

查看试题解析
21. 如图，△ABC是圆O的内接三角形，PA是圆O的切线，A为切点，PB交AC于点E，交圆O于点D，若PE=PA，∠ABC=60°，且PD=1，PB=9，求EC．

查看试题解析
22. 已知 $\vec{α}$ = $[\begin{matrix} 2 \\ 1 \end{matrix}]$ 为矩阵A= $[\begin{matrix} 1 & a \\ - 1 & 4 \end{matrix}]$ 属于λ的一个特征向量，求实数a，λ的值及A² ．

查看试题解析
23. 自极点O任意作一条射线与直线ρcosθ=3相交于点M，在射线OM上取点P，使得OM•OP=12，求动点P的极坐标方程，并把它化为直角坐标方程．

查看试题解析
24. 已知：a≥2，x∈R．求证：|x﹣1+a|+|x﹣a|≥3．

查看试题解析
25. 在公园游园活动中有这样一个游戏项目：甲箱子里装有3个白球和2个黑球，乙箱子里装有1个白球和2个黑球，这些球除颜色外完全相同；每次游戏都从这两个箱子里各随机地摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）

(1)、在一次游戏中：①求摸出3个白球的概率；②求获奖的概率；

(2)、在两次游戏中，记获奖次数为X：①求X的分布列；②求X的数学期望．

查看试题解析
26. 已知抛物线C的方程为y²=2px（p＞0），点R（1，2）在抛物线C上．

(1)、求抛物线C的方程；

(2)、过点Q（1，1）作直线交抛物线C于不同于R的两点A，B．若直线AR，BR分别交直线l：y=2x+2于M，N两点，求线段MN最小时直线AB的方程．

查看试题解析