2017年浙江省嘉兴市桐乡六中中考数学模拟试卷

试卷更新日期：2017-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. a的相反数是（）

A、|a| B、 $\frac{1}{a}$ C、﹣a D、 $\sqrt{a}$

查看试题解析
2. 下列运算正确的是（）

A、x²+x=x³ B、2x²﹣x²=1 C、x²•x=2x² D、x⁶÷x³=x³

查看试题解析
3. 式子 $\sqrt{x + 3}$ 有意义，则x的取值范围是（）

A、x≥3 B、x≤3 C、x≥﹣3 D、x≤﹣3

查看试题解析
4. 以下四个命题中真命题是（）

①三角形有且只有一个内切圆；
②四边形的内角和与外角和相等；
③顺次连接四边形各边中点所得的四边形一定是菱形；
④一组对边平行且一组对角相等的四边形是平行四边形．

A、①② B、③④ C、①②④ D、②③④

查看试题解析
5.
如图，在空白网格内将某一个小正方形涂成阴影部分，且所涂的小正方形与原阴影图形的小正方形至少有一边重合．小红按要求涂了一个正方形，所得到的阴影图形恰好是轴对称图形的概率为（　　）

A、 $\frac{1}{5}$ B、 $\frac{41}{15}$ C、 $\frac{4}{9}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图，小山岗的斜坡AC的坡角α=45°，在与山脚C距离200米的D处，测得山顶A的仰角为26.6°，小山岗的高AB约为（结果取整数，参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）（）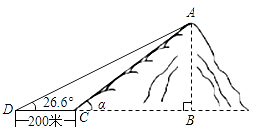

A、164m B、178m C、200m D、1618m

查看试题解析
7. 阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（）

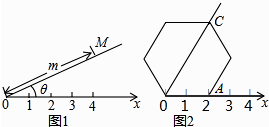A、（60°，4） B、（45°，4） C、（60°，2 $\sqrt{2}$ ） D、（50°，2 $\sqrt{2}$ ）

查看试题解析
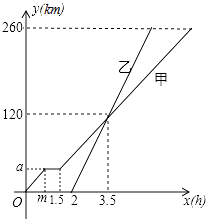
8.
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则下列结论：

①a=40，m=1；
②乙的速度是80km/h；
③甲比乙迟 $\frac{7}{4}$ h到达B地；
④乙车行驶 $\frac{9}{4}$ 小时或 $\frac{19}{4}$ 小时，两车恰好相距50km．

正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 在平面直角坐标系中，任意两点A（x₁ ， y₁），B（x₂ ， y₂），规定运算：
①A⊕B=（x₁+x₂ ， y₁+y₂）；②A⊗B=x₁x₂+y₁y₂；③当x₁=x₂且y₁=y₂时，A=B，有下列四个命题：
①若A（1，2），B（2，﹣1），则A⊕B=（3，1），A⊗B=0；
②若A⊕B=B⊕C，则A=C；
③若A⊗B=B⊗C，则A=C；
④对任意点A、B、C，均有（A⊕B）⊕C=A⊕（B⊕C）成立，其中正确命题的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

10. 在平面直角坐标系中，已知一次函数y=2x+1的图象经过P₁（x₁ ， y₁）、P₂（x₂ ， y₂）两点，若x₁＜x₂ ，则y₁y₂ ．（填“＞”“＜”或“=”）

查看试题解析
11. 分解因式：2x²﹣8x+8=

查看试题解析
12. 如图，点P（3，4），⊙P半径为2，A（2.8，0），B（5.6，0），点M是⊙P上的动点，点C是MB的中点，则AC的最小值是．

查看试题解析
13. 如图，0为原点，A（4，0），E（0，3），四边形OABC，四边形OCDE都为平行四边形，OC=5，函数y= $\frac{k}{x}$ （x＞0）的图象经过AB的中点F和DE的中点G，则k的值为．

查看试题解析

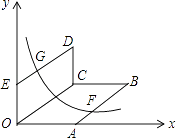
三、解答题

14. 化简求值：（ $\frac{a}{a - b}$ ﹣ $\frac{b}{a + b}$ ）÷ $\frac{a^{2} + b^{2}}{a - b}$ ，其中a=1﹣ $\sqrt{3}$ ，b=1+ $\sqrt{3}$ ．

查看试题解析
15. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．

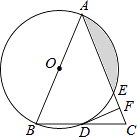(1)、求证：DF⊥AC；

(2)、若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积．

查看试题解析
16.
如果两个三角形的两条边对应相等，夹角互补，那么这两个三角形叫做互补三角形，如图2，分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF，则图中的两个三角形就是互补三角形．

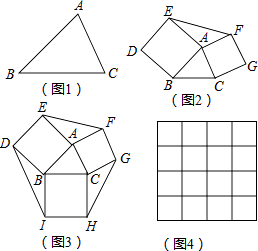(1)、图1中的△ABC的BC边上有一点D，线段AD将△ABC分成两个互补三角形，则点D在BC边的处．

(2)、证明：图2中的△ABC分割成两个互补三角形面积相等；

(3)、如图3，在图2的基础上再以BC为边向外作正方形BCHI，已知三个正方形面积分别是17、13、10．则图3中六边形DEFGHI的面积为．（提示：可先利用图4求出△ABC的面积）

查看试题解析
17.
如图，已知抛物线经过点A（2，0）和B（t，0）（t≥2），与y轴交于点C，直线l：y=x+2t经过点C，交x轴于点D，直线AE交抛物线于点E，且有∠CAE=∠CDO，作CF⊥AE于点F．

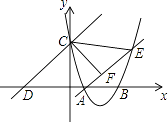(1)、求∠CDO的度数；

(2)、求出点F坐标的表达式（用含t的代数式表示）；

(3)、当S_△_COD﹣S_四边形_COAF=7时，求抛物线解析式；

(4)、当以B，C，O三点为顶点的三角形与△CEF相似时，请直接写出t的值．

查看试题解析