2016-2017学年福建省龙岩市连城二中高三上学期开学数学试卷（理科）

试卷更新日期：2017-05-09 类型：开学考试

进入出卷网下载

一、选择题

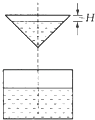
1. 集合A={﹣1，0，1}，B={y|y=cosx，x∈A}，则A∩B=（）

A、{0} B、{1} C、{0，1} D、{﹣1，0，1}

查看试题解析
2. 如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经过3分钟漏完．已知圆柱中液面上升的速度是一个常量，H是圆锥形漏斗中液面下落的高度，则H与下落时间t（分）的函数关系表示的图象只可能是（）

A、 B、 C、 D、

查看试题解析
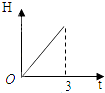3. 已知等差数列{a_n}中，a₃+a₇﹣a₁₀=8，a₁₁﹣a₄=4，记S_n=a₁+a₂+…+a_n ，则S₁₃=（）

A、78 B、152 C、156 D、168

查看试题解析
4. 已知二次曲线 $\frac{x^{2}}{4}$ + $\frac{y^{2}}{m}$ =1，则当m∈[﹣2，﹣1]时，该曲线的离心率e的取值范围是（）

A、[ $\frac{\sqrt{2}}{2}$ ， $\frac{\sqrt{3}}{2}$ ] B、[ $\frac{\sqrt{2}}{2}$ ， $\frac{\sqrt{6}}{2}$ ] C、[ $\frac{\sqrt{5}}{2}$ ， $\frac{\sqrt{6}}{2}$ ] D、[ $\frac{\sqrt{3}}{2}$ ， $\frac{\sqrt{6}}{2}$ ]

查看试题解析
5. 二项式（2x⁴﹣ $\frac{1}{3 x^{3}}$ ）ⁿ的展开式中含有非零常数项，则正整数n的最小值为（）

A、7 B、12 C、14 D、5

查看试题解析
6. 若a= $\int \begin{array}{l} 2 \\ 0 \end{array} x^{2} d x$ ，b= $\int \begin{array}{l} 2 \\ 0 \end{array} x^{3} d x$ ，c= $\int \begin{array}{l} 2 \\ 0 \end{array} \sin x d x$ ，则a，b，c大小关系是（）

A、a＜c＜b B、a＜b＜c C、c＜b＜a D、c＜a＜b

查看试题解析
7. 已知 $\vec{a} ， \vec{b}$ 均为非零向量，条件p： $\vec{a} \cdot \vec{b} > 0$ ，条件q： $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角，则p是q成立的（）

A、充要条件 B、充分而不必要的条件 C、必要而不充分的条件 D、既不充分也不必要的条件

查看试题解析
8. 从数字1，2，3，4，5中任取两个不同的数字构成一个两位数，这个两位数大于40的概率（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 在空间中，有如下命题：
①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；
②若平面α∥平面β，则平面α内任意一条直线m∥平面β；
③若平面α与平面β的交线为m，平面α内的直线n⊥直线m，则直线n⊥平面β；
④若平面α内的三点A、B、C到平面β的距离相等，则α∥β．
其中正确命题的个数为（）个．

A、0 B、1 C、2 D、3

查看试题解析
10. 设动直线x=a与函数f（x）=2sin²（ $\frac{π}{4}$ +x）和g（x）= $\sqrt{3}$ cos2x的图象分别交于M、N两点，则|MN|的最大值为（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、2 D、3

查看试题解析
11. 已知函数y=log_a（ax²﹣x）在区间[2，4]上是增函数，则实数a的取值范围是（）

A、（ $\frac{1}{4} ， 1$ ）∪（1，+∞） B、（1，+∞） C、 $(\frac{1}{4} ， 1)$ D、（0， $\frac{1}{8}$ ）

查看试题解析
12. 若二次函数y=f（x）的图象过原点，且它的导数y=f′（x）的图象是经过第一、二、三象限的一条直线，则y=f（x）的图象顶点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题

13. 有一个几何体的三视图及其尺寸（单位cm），则该几何体的表面积为：．

查看试题解析
14. 不等式 $| x + \frac{1}{x} | > | a - 5 | + 1$ 对于一切非零实数x均成立，则实数a的取值范围是．

查看试题解析
15. 设x、y满足约束条件 ${\begin{matrix} x \geq 0 \\ x \geq y \\ 2 - y \leq 1 \end{matrix}$ ，则z=3x+2y的最大值是．

查看试题解析
16. 对于函数 ①f（x）=lg（|x﹣2|+1），②f（x）=（x﹣2）² ， ③f（x）=cos（x+2）．给出如下三个命题：
命题甲：f（x+2）是偶函数；
命题乙：f（x）在区间（﹣∞，2）上是减函数，在区间（2，+∞）上是增函数；
命题丙：f（x+2）﹣f（x）在（﹣∞，+∞）上是增函数．
能使命题甲、乙、丙均为真的所有函数的序号是．

查看试题解析

三、解答题

17. 在外接圆直径为1的△ABC中，角A，B，C的对边分别为a，b，c，设向量 $\vec{π}$ =（a，cosB）， $\vec{n}$ =（b，cosA），且 $\vec{π}$ ∥ $\vec{n}$ ， $\vec{π}$ ≠ $\vec{n}$ ．

(1)、求sinA+sinB的取值范围；

(2)、若abx=a+b，试确定实数x的取值范围．

查看试题解析
18. 数列{a_n}的前n项和记为S_n ， a₁=t，a_n₊₁=2S_n+1（n∈N^*）．

(1)、当t为何值时，数列{a_n}为等比数列？

(2)、在（1）的条件下，若等差数列{b_n}的前n项和T_n有最大值，且T₃=15，又a₁+b₁ ， a₂+b₂ ， a₃+b₃成等比数列，求T_n ．

查看试题解析
19. 如图，已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 $\frac{A E}{A C} = \frac{A F}{A D}$ =λ（0＜λ＜1）

(1)、求证：不论λ为何值，总有EF⊥平面ABC：

(2)、若λ= $\frac{1}{2}$ ，求三棱锥A﹣BEF的体积．

查看试题解析
20. 某班从6名干部中（其中男生4人，女生2人）选3人参加学校的义务劳动．

(1)、设所选3人中女生人数为ξ，求ξ的分布列及Eξ；

(2)、求男生甲或女生乙被选中的概率；

(3)、在男生甲被选中的情况下，求女生乙也被选中的概率．

查看试题解析
21. 已知两点M和N分别在直线y=mx和y=﹣mx（m＞0）上运动，且|MN|=2，动点p满足： $2 \vec{O P} = \vec{O M} + \vec{O N}$ （O为坐标原点），点P的轨迹记为曲线C．
（I）求曲线C的方程，并讨论曲线C的类型；
（Ⅱ）过点（0，1）作直线l与曲线C交于不同的两点A、B，若对于任意m＞1，都有∠AOB为锐角，求直线l的斜率k的取值范围．

查看试题解析
22. 设函数f（x）= $x - \frac{1 n (1 + x)}{1 + x}$

(1)、令N（x）=（1+x）²﹣1+ln（1+x），判断并证明N（x）在（﹣1，+∞）上的单调性，并求N（0）；

(2)、求f（x）在定义域上的最小值；

(3)、是否存在实数m，n满足0≤m＜n，使得f（x）在区间[m，n]上的值域也为[m，n]？
（参考公式：[ln（1+x）′]= $\frac{1}{1 + x}$ ）

查看试题解析