2017年浙江省湖州四中教育集团中考数学一模试卷
试卷更新日期:2017-05-09 类型:中考模拟
一、选择题
-
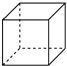
1. ﹣5的相反数是( )A、﹣5 B、5 C、﹣ D、2. 下面几个几何体,主视图是圆的是( )A、
 B、
B、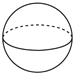 C、
C、 D、
D、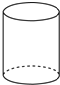 3. 如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )
3. 如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )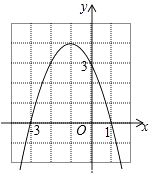 A、二次函数y=ax2+bx+c的最大值为4 B、常数项c为3 C、一元二次方程ax2+bx+c=0的两根之和为﹣2 D、使y≤3成立的x的取值范围是x≥04. 如图,河堤横断面迎水坡AB的坡比是1: ,堤高BC=10m,则坡面AB的长度是(
A、二次函数y=ax2+bx+c的最大值为4 B、常数项c为3 C、一元二次方程ax2+bx+c=0的两根之和为﹣2 D、使y≤3成立的x的取值范围是x≥04. 如图,河堤横断面迎水坡AB的坡比是1: ,堤高BC=10m,则坡面AB的长度是(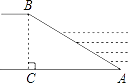 A、15m B、20 m C、20m D、10 m5. 为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如表:
A、15m B、20 m C、20m D、10 m5. 为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如表:每天使用零花钱(单位:元)
1
2
3
4
5
人数
2
5
8
9
6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A、4,3 B、4,3.5 C、3.5,3.5 D、3.5,46. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )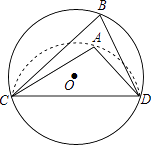 A、100° B、80° C、60° D、50°7. 在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A( ,0)、B(3 ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )A、2 ﹣2 B、2 C、2 D、28. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
A、100° B、80° C、60° D、50°7. 在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A( ,0)、B(3 ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )A、2 ﹣2 B、2 C、2 D、28. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )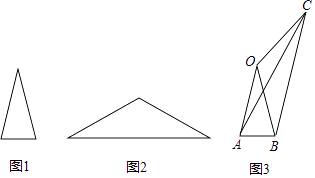 A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=4
A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=4二、填空题
-
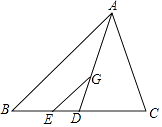
9. 若分式 有意义,则x的取值范围为 .10. 已知α是锐角,tanα=2cos30°,那么α=度.11. 为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为S甲2=3.6,S乙2=15.8,则种小麦的长势比较整齐.12. 如图,点G是△ABC的重心,联结AG并延长交BC于点D,GE∥AB交BC与E,若AB=6,那么GE= .
 13. 如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣ x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
13. 如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣ x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .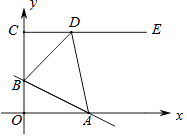 14. 阅读下面材料:
14. 阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:当x=﹣3或1时,y1=y2 .
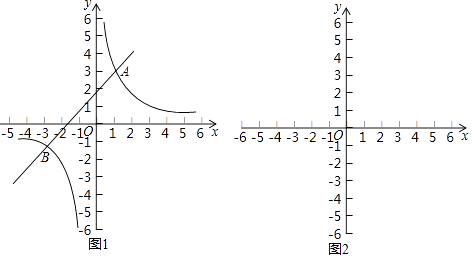 (1)、通过观察函数的图象,可以得到不等式ax+b> 的解集 .(2)、参考观察函数的图象方法,解决问题:关于x的不等式x2+a﹣ <0(a>0)只有一个整数解,则a的取值范围 .
(1)、通过观察函数的图象,可以得到不等式ax+b> 的解集 .(2)、参考观察函数的图象方法,解决问题:关于x的不等式x2+a﹣ <0(a>0)只有一个整数解,则a的取值范围 .三、解答题
-
15. 计算:(π﹣2016)0+|1﹣ |+2﹣1﹣2sin45°.16. 解方程: .17. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
 18. 2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
18. 2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.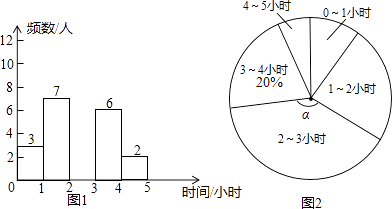
根据上述信息,解答下列问题:
(1)、本次抽取的学生人数是;扇形统计图中的圆心角α等于;补全统计直方图;(2)、被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.19. 如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.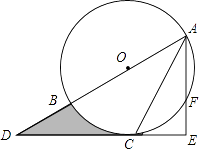 (1)、求证:DE是⊙O的切线;(2)、若AE=6,∠D=30°,求图中阴影部分的面积.20. 某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)、求证:DE是⊙O的切线;(2)、若AE=6,∠D=30°,求图中阴影部分的面积.20. 某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.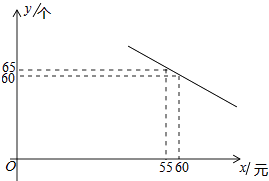 (1)、试确定y与x之间的函数关系式;(2)、若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?(3)、若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.21. 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造▱OACD,设点P的横坐标为m.
(1)、试确定y与x之间的函数关系式;(2)、若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?(3)、若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.21. 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造▱OACD,设点P的横坐标为m.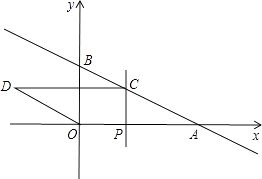 (1)、求直线AB的函数表达式;(2)、若四边形OACD恰是菱形,请求出m的值;(3)、在(2)的条件下,y轴的正半轴上是否存在点Q,连结CQ,使得∠OQC+∠ODC=180°.若存在,直接写出所有符合条件的点Q的坐标,若不存在,则说明理由.22. 在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.
(1)、求直线AB的函数表达式;(2)、若四边形OACD恰是菱形,请求出m的值;(3)、在(2)的条件下,y轴的正半轴上是否存在点Q,连结CQ,使得∠OQC+∠ODC=180°.若存在,直接写出所有符合条件的点Q的坐标,若不存在,则说明理由.22. 在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.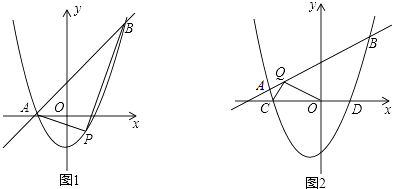 (1)、如图1,当k=1时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
(1)、如图1,当k=1时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.