2017年新疆乌鲁木齐九十八中中考数学一模试卷
试卷更新日期：2017-05-09 类型：中考模拟
一、一.选择题
-
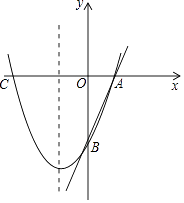
1. ﹣ 的相反数是（ ）A、4 B、﹣ C、 D、﹣42. 把a3﹣ab2分解因式的正确结果是（ ）A、（a+ab）（a﹣ab） B、a（a2﹣b2） C、a（a+b）（a﹣b） D、a（a﹣b）23. 新疆近年旅游业发展快速，每年都吸引众多海内外游客前来观光、旅游，据有关部门统计报道：2016年全疆共接待游客3354万人次，将3354万用科学记数法表示为（ ）A、3.354×106 B、3.354×107 C、3.354×108 D、33.54×1064. 对于函数y=﹣k2x（k是常数，k≠0）的图象，下列说法不正确的是（ ）A、是一条直线 B、过点（ ，﹣k） C、经过一、三象限或二、四象限 D、y随着x增大而减小5. 在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（ ）A、 B、 C、 D、6. 抛物线y=﹣（a﹣8）2+2的顶点坐标是（ ）A、（ 2，8 ） B、（ 8，2 ） C、（﹣8，2 ） D、（﹣8，﹣2）7. 若关于x的一元二次方程kx2﹣4x+3=0有实数根，则k的非负整数值是（ ）A、1 B、0，1 C、1，2 D、1，2，38. 若不等式组 的解集是x＞3，则m的取值范围是（ ）A、m＞3 B、m≥3 C、m≤3 D、m＜39. 如图，A是反比例函数y= 图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为2，则k的值为（ ）
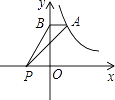A、1 B、2 C、3 D、410. △ABC是⊙O内接三角形，∠BOC=80°，那么∠A等于（ ）A、80° B、40° C、140° D、40°或140°二、二.填空题
-
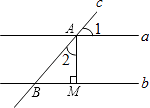
11. 的平方根是 ．12. 若一个多边形内角和为900°，则这个多边形是边形．13. 函数y= 中自变量x的取值范围是 ．14. 如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为点M，若∠1=58°，则∠2= ．
15. 如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=42°，则∠OAC的度数是 ．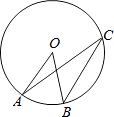
16.用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第n个图案中共有小三角形的个数是 ．
三、三.解答题
-
17. 计算： ．18. 化简，求值： ，其中m= ．19. 解方程组 ．20. 某校实施新课程改革以来，学生的学习能力有了很大提高．王老师为进一步了解本班学生自主学习、合作交流的现状，对该班部分学生进行调查，把调查结果分为四类（A．特别好，B．好，C．一般，D．较差）后，再将调查结果绘制成两幅不完整的统计图（如图）．请根据统计图解答下列问题：
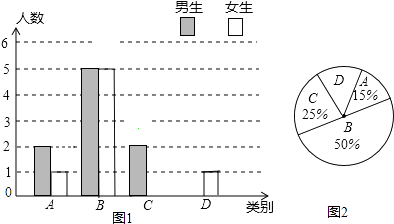(1)、本次调查中，王老师一共调查了名学生；(2)、将两幅统计图中不完整的部分补充完整；(3)、假定全校各班实施新课程改革效果一样，全校共有学生2 400人，请估计该校新课程改革效果达到A类的有多少学生；(4)、为了共同进步，王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习，请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率．21. 如图，PA、PB分别与⊙O相切于点A、B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N．
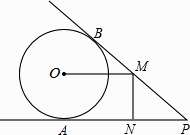(1)、求证：OM=AN；(2)、若⊙O的半径R=3，PA=9，求OM的长．22. 某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆，已知大型客车每辆62万元，中型客车每辆40万元，设购买大型客车x（辆），购车总费用为y（万元）．(1)、求y与x的函数关系式（不要求写出自变量x的取值范围）；(2)、若购买中型客车的数量少于大型客车的数量，请你给出一种费用最省的方案，并求 出该方案所需费用．
