2017年山东省日照市经济开发区中考数学一模试卷
试卷更新日期:2017-05-09 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、3﹣2 B、 C、|﹣ | D、2. 以下是我市著名企事业(新飞电器、心连心化肥、新乡银行、格美特科技)的徽标或者商标,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2014年巴西世界杯在南美洲国家巴西境内12座城市中的12座球场内举行,本届世界杯的冠军将获得3500万美元的奖励,将3500万用科学记数法表示为( )A、3.5×106 B、3.5×107 C、35×106 D、0.35×1084. 下列各式计算正确的是( )A、 =1 B、a6÷a2=a3 C、x2+x3=x5 D、(﹣x2)3=﹣x65.
3. 2014年巴西世界杯在南美洲国家巴西境内12座城市中的12座球场内举行,本届世界杯的冠军将获得3500万美元的奖励,将3500万用科学记数法表示为( )A、3.5×106 B、3.5×107 C、35×106 D、0.35×1084. 下列各式计算正确的是( )A、 =1 B、a6÷a2=a3 C、x2+x3=x5 D、(﹣x2)3=﹣x65.用6个完全相同的小正方体组合成如图所示的立体图形,它的俯视图为( )
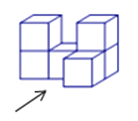 A、
A、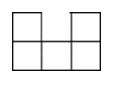 B、
B、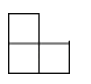 C、
C、 D、
D、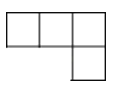 6. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( )
6. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( ) A、8,6 B、8,5 C、52,53 D、52,527. 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
A、8,6 B、8,5 C、52,53 D、52,527. 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )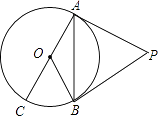 A、60° B、62° C、31° D、70°8. 若不等式组 有解,则a的取值范围是( )A、a>﹣1 B、a≥﹣1 C、a≤1 D、a<19. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
A、60° B、62° C、31° D、70°8. 若不等式组 有解,则a的取值范围是( )A、a>﹣1 B、a≥﹣1 C、a≤1 D、a<19. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )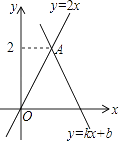 A、x>0 B、0<x<1 C、1<x<2 D、x>210. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )A、m≤2或m≥3 B、m≤3或m≥4 C、2<m<3 D、3<m<411. 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
A、x>0 B、0<x<1 C、1<x<2 D、x>210. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )A、m≤2或m≥3 B、m≤3或m≥4 C、2<m<3 D、3<m<411. 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )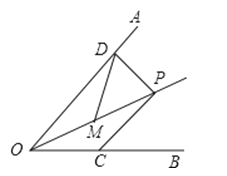 A、2 B、2 C、4 D、412. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是( )
A、2 B、2 C、4 D、412. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是( ) A、(2011,0) B、(2011,1) C、(2011,2) D、(2010,0)
A、(2011,0) B、(2011,1) C、(2011,2) D、(2010,0)二、填空题
-
13. 计算:( +π)0﹣2|1﹣sin30°|+( )﹣1= .14. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是 .
 15. 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 .
15. 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 .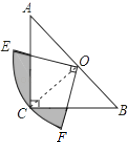 16. 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为 .
16. 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为 .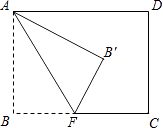
三、解答题
-
17. 先化简,再求值:(a+ )÷(a﹣2+ ),其中a满足a2﹣a﹣2=0.18. 在2015年的政府工作报告中提出了九大热词,某数学兴趣小组就A互联网+、B民生底线、C中国制造2.0、D能耗强度等四个热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
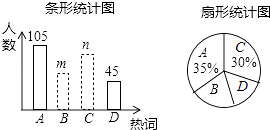
请你根据统计图提供的信息,解答下列问题:
(1)、本次调查中,一共调查了名同学;(2)、条形统计图中,m= , n=;(3)、扇形统计图中,热词B所在扇形的圆心角的度数是;(4)、从该校学生中随机抽取一个最关注热词D的学生的概率是多少?19. 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒. (1)、若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;(2)、当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.20. 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 千米的C处.
(1)、若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;(2)、当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.20. 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 千米的C处.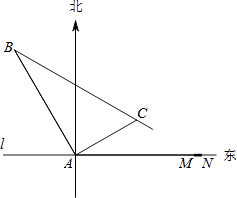 (1)、该飞机航行的速度是多少千米/小时?(结果保留根号)(2)、如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.21. 问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(1)、该飞机航行的速度是多少千米/小时?(结果保留根号)(2)、如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.21. 问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系. (1)、【发现证明】
(1)、【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(2)、【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.
(3)、【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: =1.41, =1.73)
22. 如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.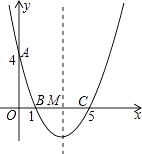 (1)、求抛物线的解析式和对称轴;(2)、在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和对称轴;(2)、在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.