2017年江苏省扬州市仪征市南师大二附中中考数学一模试卷
试卷更新日期:2017-05-09 类型:中考模拟
一、选择题
-
1. 是( )A、整数 B、无理数 C、有理数 D、自然数2. 下列式子正确的是( )A、a2+a3=a5 B、(a2)3=a5 C、a+2b=2ab D、(﹣ab)2=a2b23. 人体中红细胞的直径约为0.0000077m,用科学记数法表示数的结果是( )A、0.77×10﹣5m B、0.77×10﹣6m C、7.7×10﹣5m D、7.7×10﹣6m4. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、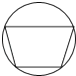 C、
C、 D、
D、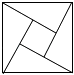 5. 如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )
5. 如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )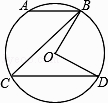 A、80° B、50° C、40° D、20°6. 无论m为何值,点A(m,5﹣2m)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7.
A、80° B、50° C、40° D、20°6. 无论m为何值,点A(m,5﹣2m)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
 A、70° B、35° C、40° D、50°8. 方程x2﹣ +1=﹣4x的正数根的取值范围是( )A、0<x<1 B、1<x<2 C、2<x<3 D、3<x<4
A、70° B、35° C、40° D、50°8. 方程x2﹣ +1=﹣4x的正数根的取值范围是( )A、0<x<1 B、1<x<2 C、2<x<3 D、3<x<4二、填空题
-
9. 分解因式:2x2﹣8= .10. 当x=时,分式 无意义.11. 仪征市某活动中心组织一次少年跳绳比赛,各年龄组的参赛人数如表所示:
年龄组
12岁
13岁
14岁
15岁
参赛人数
5
19
13
13
则全体参赛选手年龄的中位数是岁.
12. 若a+b=2,则代数式3﹣2a﹣2b= .13. 一个圆锥的侧面展开图是半径为3,圆心角为120°的扇形,则这个圆锥的高为 .14. 如图,直线AlA∥BB1∥CC1 , 若AB=8,BC=4,A1B1=6,则线段A1C1的长是 . 15. 关于的一元二次方程kx2﹣x+1=0有两个实数根,则k的取值范围是 .16. 如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是 .
15. 关于的一元二次方程kx2﹣x+1=0有两个实数根,则k的取值范围是 .16. 如图,用若干个全等的正五边形可以拼成一个环状,如图是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是 . 17. 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N.若CM=3,AN=4,则tan∠CAN的值为 .
17. 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N.若CM=3,AN=4,则tan∠CAN的值为 .
三、解答题
-
18. 化简计算(1)、计算:﹣2﹣2+ sin45°﹣|1﹣ |(2)、解不等式组: .19. 先化简,再求值: ÷(1﹣ ),其中m满足一元二次方程m2﹣4m+3=0.20. “低碳环保,你我同行”.仪征市区的公共自行车给市民出行带来不少方便.我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:
A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.
将这次调查情况整理并绘制如下两幅统计图:

根据图中的信息,解答下列问题:
(1)、本次活动共有位市民参与调查;(2)、补全条形统计图;(3)、根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人?21. 我校“文化氧吧”有A、B、C、D四本书是小明想拜读的,但他现阶段只打算选读两本.(1)、若小明已选A书,再从其余三本书中随机选一款,恰好选中C的概率是;(2)、小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率.22.已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
 (1)、求证:△ABM≌△CDN;(2)、矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.23. 甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?24. 在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.(1)、如图①,求证直线DE是⊙O的切线;
(1)、求证:△ABM≌△CDN;(2)、矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.23. 甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?24. 在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.(1)、如图①,求证直线DE是⊙O的切线; (2)、如图②,作DG⊥AB于H,交⊙O于G,若AB=5,AC=8,求DG的长.
(2)、如图②,作DG⊥AB于H,交⊙O于G,若AB=5,AC=8,求DG的长. 25.
25.如图,已知∠ABM=37°,AB=20,C是射线BM上一点.
 (1)、求点A到BM的距离;(2)、在下列条件中,可以唯一确定BC长的是;(填写所有符合条件的序号)
(1)、求点A到BM的距离;(2)、在下列条件中,可以唯一确定BC长的是;(填写所有符合条件的序号)①AC=13;②tan∠ACB= ;③连接AC,△ABC的面积为126.
(3)、在(2)的答案中,选择一个作为条件,画出草图,求BC.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
26. 阅读下面材料:实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.

解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,
设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l22=(AB+BC)2=(5+10)2=225.
为比较l1 , l2的大小,我们采用“作差法”:
∵l12﹣l22=25(π2﹣8)>0∴l12>l22∴l1>l2 ,
小明认为应选择路线2较短.
(1)、问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”.请你用上述方法帮小亮比较出l1与l2的大小:
(2)、问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当 满足什么条件时,选择路线2最短?请说明理由.
(3)、问题解决:如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式).
27.先让我们一起来学习方程m2+1= 的解法:
解:令m2=a,则a+1= ,方程两边平方可得,(a+1)2=a+3
解得a1=1,a2=﹣2,∵m2≥0∴m2=1∴m=±1
点评:类似的方程可以用“整体换元”的思想解决.
不妨一试:
如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
 (1)、求抛物线的解析式;(2)、①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);(3)、当△PHO为等边三角形时,求点P坐标;(4)、如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);(3)、当△PHO为等边三角形时,求点P坐标;(4)、如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.