2017年江苏省泰州市兴化市陶庄中心校中考数学一模试卷
试卷更新日期:2017-05-08 类型:中考模拟
一、选择题
-
1. 4的平方根是( )A、8 B、2 C、±2 D、±2. 把数7700000用科学记数法表示为( )A、0.77×106 B、7.7×106 C、0.77×107 D、7.7×1073. 如图,AB∥CD,∠DCE=80°,则∠BEF=( )
 A、100° B、90° C、80° D、70°4. 点M(﹣4,﹣1)关于y轴对称的点的坐标为( )A、(﹣4,1) B、(4,1) C、(4,﹣1) D、(﹣4,﹣1)5. 式子y= 中x的取值范围是( )A、x≥0 B、x≥0且x≠1 C、0≤x<1 D、x>16. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
A、100° B、90° C、80° D、70°4. 点M(﹣4,﹣1)关于y轴对称的点的坐标为( )A、(﹣4,1) B、(4,1) C、(4,﹣1) D、(﹣4,﹣1)5. 式子y= 中x的取值范围是( )A、x≥0 B、x≥0且x≠1 C、0≤x<1 D、x>16. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 已知某圆锥的底面圆的半径r=2cm,将圆锥侧面展开得到一个圆心角θ=120°的扇形,则该圆锥的母线长l为( )A、3cm B、4cm C、5cm D、6cm8. 关于x的不等式x﹣b≥0恰有两个负整数解,则b的取值范围是( )A、﹣3<b<﹣2 B、﹣3<b≤﹣2 C、﹣3≤b≤﹣2 D、﹣3≤b<﹣29. 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
7. 已知某圆锥的底面圆的半径r=2cm,将圆锥侧面展开得到一个圆心角θ=120°的扇形,则该圆锥的母线长l为( )A、3cm B、4cm C、5cm D、6cm8. 关于x的不等式x﹣b≥0恰有两个负整数解,则b的取值范围是( )A、﹣3<b<﹣2 B、﹣3<b≤﹣2 C、﹣3≤b≤﹣2 D、﹣3≤b<﹣29. 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( ) A、3 km B、3 km C、4 km D、(3 ﹣3)km10. 如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A、3 km B、3 km C、4 km D、(3 ﹣3)km10. 如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )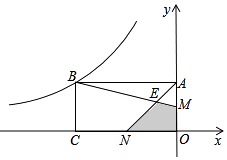 A、y=﹣ B、y=﹣ C、y=﹣ D、y=﹣
A、y=﹣ B、y=﹣ C、y=﹣ D、y=﹣二、填空题
-
11. (﹣p)2•(﹣p)3= .12. 分解因式:x2y﹣4xy+4y= .13. 若3是关于x的方程x2﹣x+c=0的一个根,则方程的另一个根等于 .14. 布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,摸出的球是白球的概率是 .15. 已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长5cm,那么这个三角形的腰长为cm.16. 如图所示,以锐角△ABC的边AB为直径作⊙O,交AC,BC于E、D两点,若AC=14,CD=4,7sinC=3tanB,则BD= .
 17. 如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于 .
17. 如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于 . 18. 已知关于x的二次函数y=ax2+2ax+a﹣3在﹣2≤x≤2时的函数值始终是负的,则常数a的取值范围是 .
18. 已知关于x的二次函数y=ax2+2ax+a﹣3在﹣2≤x≤2时的函数值始终是负的,则常数a的取值范围是 .三、解答题
-
19. 结算下列各题(1)、计算:| ﹣2|+( )﹣1﹣(π﹣3.14)0﹣ ;(2)、计算:[xy(3x﹣2)﹣y(x2﹣2x)]÷x2y.20. 先化简,再求值:( + )÷ ,其中x= ﹣1.21. 如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
 22. 某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.(1)、小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是;(2)、据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、92、85.
22. 某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.(1)、小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是;(2)、据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、92、85.①这组数据的众数是 , 中位数是;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人 ?
23. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
 24. 某市为了美化城市,计划在某段公路旁栽480棵树,由于有志愿者的支援,实际每天栽树比原计划多 ,结果提前4天完成任务.请根据以上信息,提出一个能用分式方程解决的问题,并写出这个问题的解答过程.25. 如图,直线y1=kx+b与双曲线y2= 交于A、B两点,它们的横坐标分别为1和5.
24. 某市为了美化城市,计划在某段公路旁栽480棵树,由于有志愿者的支援,实际每天栽树比原计划多 ,结果提前4天完成任务.请根据以上信息,提出一个能用分式方程解决的问题,并写出这个问题的解答过程.25. 如图,直线y1=kx+b与双曲线y2= 交于A、B两点,它们的横坐标分别为1和5. (1)、当m=5时,求直线AB的解析式及△AOB的面积;(2)、当y1>y2时,直接写出x的取值范围.26.
(1)、当m=5时,求直线AB的解析式及△AOB的面积;(2)、当y1>y2时,直接写出x的取值范围.26.如图①所示,空圆柱形容器内放着一个实心的“柱锥体”(由一个圆柱和一个同底面的圆锥组成的几何体).现向这个容器内匀速注水,水流速度为5cm3/s,注满为止.已知整个注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请你根据图中信息,解答下列问题:
 (1)、圆柱形容器的高为cm,“柱锥体”中圆锥体的高为cm;(2)、分别求出圆柱形容器的底面积与“柱锥体”的底面积.27. 如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
(1)、圆柱形容器的高为cm,“柱锥体”中圆锥体的高为cm;(2)、分别求出圆柱形容器的底面积与“柱锥体”的底面积.27. 如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒. (1)、求证四边形ABCD是平行四边形;(2)、当△BEP为等腰三角形时,求t2﹣31t的值;(3)、当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与▱ABCD重叠部分的面积.28. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)、求证四边形ABCD是平行四边形;(2)、当△BEP为等腰三角形时,求t2﹣31t的值;(3)、当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与▱ABCD重叠部分的面积.28. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.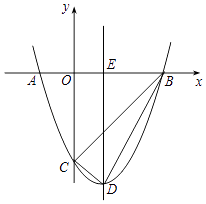 (1)、求证△BCD是直角三角形;(2)、点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;(3)、点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
(1)、求证△BCD是直角三角形;(2)、点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;(3)、点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.