2017年江苏省南通市通州区中考数学一模试卷
试卷更新日期：2017-05-08 类型：中考模拟
一、选择题
-
1. 二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标是（ ）A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（﹣1，﹣3）2. 当二次函数y=x2+4x+9取最小值时，x的值为（ ）A、﹣2 B、1 C、2 D、93. 二次函数y=x2+2x+2与坐标轴的交点个数是（ ）A、0个 B、1个 C、2个 D、3个4. 为搞好环保，某公司准备修建一个长方体的污水处理池，池底矩形的周长为100m，则池底的最大面积是（ ）A、600 m2 B、625 m2 C、650 m2 D、675 m25. 设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+a上的三点，则y1 ， y2 ， y3的大小关系为（ ）A、y1＞y2＞y3 B、y1＞y3＞y2 C、y3＞y2＞y1 D、y3＞y1＞y26. 如图，直径为10的⊙A经过点C和点O，点B是y轴右侧⊙A优弧上一点，∠OBC=30°，则点C的坐标为（ ）
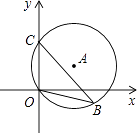A、（0，5） B、（0，5 ） C、（0， ） D、（0， ）7. 一个点到圆的最小距离为6cm，最大距离为9cm，则该圆的半径是（ ）A、1.5cm B、7.5cm C、1.5cm或7.5cm D、3cm或15cm8. 如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为（ ）
A、2cm B、 cm C、2 cm D、二、填空题
-
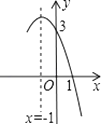
9. 如果抛物线y=（m﹣1）x2的开口向上，那么m的取值范围是 ．10. 抛物线y=ax2+3与x轴的两个交点分别为（m，0）和（n，0），则当x=m+n时，y的值为 ．11. 将二次函数y=x2﹣2x+m的图象向下平移1个单位后，它的顶点恰好落在x轴上，则m= ．12. 抛物线y=﹣x2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是 ．
13. 如图，AB是⊙O的直径，CD为弦，CD⊥AB于E，若CD=6，BE=1，则⊙O的直径为 ．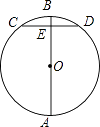
14. 如图所示，点A是半圆上一个三等分点，点B是 的中点，点P是直径 MN上一动点，若⊙O的直径为2，则AP+BP的最小值是 ．
15. 如图，AB是⊙O的直径，∠C=30°，则∠ABD等于 ．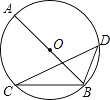
16. 在半径为5cm的圆中，两条平行弦的长度分别为6cm和8cm，则这两条弦之间的距离为 ．三、解答题
-
17. 计算： ．18. 已知二次函数y=ax2+bx+c的图象经过A（﹣1，0），B（3，0），C（0，﹣3）三点，求这个二次函数的解析式．19. 已知：如图，AB是⊙O的弦，半径OC、OD分别交AB于点E、F，且OE=OF．
求证：AE=BF．
20.如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．
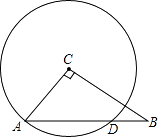21. 如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．
(1)、若BE=8，求⊙O的半径；(2)、若∠DMB=∠D，求线段OE的长．22. 已知二次函数y=﹣2x2+4x+6．(1)、求出该函数图象的顶点坐标，图象与x轴的交点坐标．(2)、当x在什么范围内时，y随x的增大而增大？(3)、当x在什么范围内时，y≤6？23.如图，直线AB分别交y轴、x轴于A、B两点，OA=2，tan∠ABO= ，抛物线y=﹣x2+bx+c过A、B两点．
(1)、求直线AB和这个抛物线的解析式；(2)、设抛物线的顶点为D，求△ABD的面积；(3)、作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN的长度l有最大值？最大值是多少？24. 某衬衣店将进价为30元的一种衬衣以40元售出，平均每月能售出600件，调查表明：这种衬衣售价每上涨1元，其销售量将减少10件．(1)、写出月销售利润y（单位：元）与售价x（单位：元/件）之间的函数解析式．(2)、当销售价定为45元时，计算月销售量和销售利润．(3)、衬衣店想在月销售量不少于300件的情况下，使月销售利润达到10000元，销售价应定为多少？(4)、当销售价定为多少元时会获得最大利润？求出最大利润．