广东省潮州市潮安区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-04-12 类型：期末考试
一、选择题
-
1. （- ）-1＝（ ）A、 B、 C、3 D、-32. 芝麻作为食品和药物，均广泛使用，经测算，一粒芝麻重量约有0.00 000 201kg，用科学记数法表示10粒芝麻的重量为（ ）A、2.01×10-6kg B、2.01×10-5kg C、20.1×10-7kg D、20.1×10-6kg3. 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（ ）A、
B、
C、
D、
4. 已知△ABC中，∠A＝20°，∠B＝70°，那么△ABC是（ ）A、直角三角形 B、锐角三角形 C、钝角三角形 D、正三角形5. 一个三角形的三边长分别为x、2、3，那么x的取值范围是（ ）A、2＜x＜3 B、1＜x＜5 C、2＜x＜5 D、x＞26. 下列各式中计算正确的是（ ）A、t10÷t9＝t B、（xy2）3＝xy6 C、（a3）2＝a5 D、x3x3＝2x67. 如图，已知AB∥CD，CE交AB于点F，若∠E＝20°，∠C＝45°，则∠A的度数为（ ）
A、5° B、15° C、25° D、35°8. 图中的三角形被木板遮住了一部分，这个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能9. 下列式子从左到右的变形一定正确的是（ ）
A、 = B、 = C、 = D、 =10. 根据下列已知条件，能唯一画出△ABC的是（ ）A、AB＝5，BC＝3，AC＝8 B、AB＝4，BC＝3，∠A＝30° C、∠C＝90°，AB＝6 D、∠A＝60°，∠B＝45°，AB＝4二、填空题
-
11. 计算：-y2•（-y）3•（-y）4＝ ．12. 当x＝2018时，分式 的值为 ．13. 如图，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，若PC＝4，则PD的长为 ．
14. 若a2+b2＝12，ab＝-3，则（a-b）2的值应为 ．15. 将正三角形、正四边形、正五边形按如图所示的位置摆放．如果∠3＝30°，那么∠1+∠2＝°
16. 用4块完全相同的长方形拼成正方形（如图），用不同的方法，计算图中阴影部分的面积，可得到1个关于a，b的等式为 ．
三、解答题
-
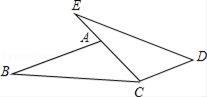
17. 分解因式：(1)、m2-4mn+4n2(2)、2x2-18．18. 计算：（x-2）（x+5）-x（x-2）．19. 已知：如图，点E，A，C在同一直线上，AB∥CD，AB＝CE，AC＝CD．
求证：BC＝ED．
20. 如图，在平面直角坐标系中，点A（4，4），B（2，-4）．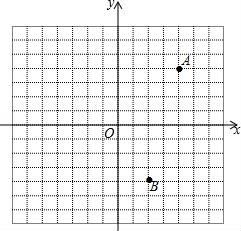
(1)、若点A关于x轴、y轴的对称点分别是点C、D，请分别描出并写出点C、D的坐标；(2)、在y轴上求作一点P，使PA+PB最小（不写作法，保留作图痕迹）21. 已知a2-2a-2＝0，求代数式 的值．22. 某内陆城市为了落实国家“一带一路”倡议，促进经济发展，增强对外贸易的竞争力，把距离港口420km的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2h，求汽车原来的平均速度．23. 如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.
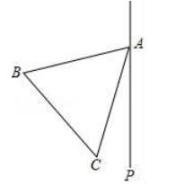(1)、依题意补全图形；
(2)、若∠PAC＝20°，求∠AEB的度数；
(3)、连结CE，写出AE， BE， CE之间的数量关系，并证明你的结论．
24. 观察探索：①（x-1）（x+1）＝x2-1
②（x-1）（x2+x+1）＝x3-1
③（x-1）（x3+x2+x+1）＝x4-1
④（x-1）（x4+x3+x2+x+1）＝x5-1
…
(1)、根据规律写出第⑤个等式：；(2)、求27+26+25+24+23+22+2的值；(3)、请求出22018+22017+22016+…+22+2的个位数字．25. 在△ABC中，AB＝AC，∠BAC＝100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．
(1)、求∠DFG的度数；(2)、设∠BAD＝θ，①当θ为何值时，△DFG为等腰三角形；
②△DFG有可能是直角三角形吗？若有，请求出相应的θ值；若没有，请说明理由．