山西省吕梁市2019届高三上学期文数第一次模拟考试试卷
试卷更新日期:2019-04-12 类型:高考模拟
一、单选题
-
1. 集合 , ,则 的元素个数( )A、3 B、4 C、5 D、62. 已知复数 ,则 ( )A、 B、 C、 D、53. 设 :关于 的方程 有解; :关于 的不等式 对于 恒成立,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 我国古代数学家刘徽创立了“割圆术”用于计算圆周率 的近似值,即用圆内接正 边形的面积代替圆的面积,当 无限增大时,多边形的面积无限接近圆的面积。设 是圆内接正十二边形,在一次探究中,某同学在圆内随机撒一把米(共100粒),统计出正十二边形 内有95粒,则可以估计 的近似值为( )A、 B、 C、 D、5. 某几何体的三视图如图所示,则该几何体的表面积是( )
 A、 B、 C、 D、6. 函数 的图象大致为( )A、
A、 B、 C、 D、6. 函数 的图象大致为( )A、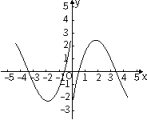 B、
B、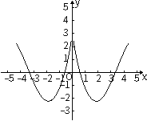 C、
C、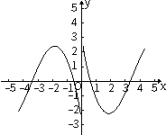 D、
D、 7. 执行下面的程序框图,为使输出 等于1,则输入的 值为( )
7. 执行下面的程序框图,为使输出 等于1,则输入的 值为( ) A、 或4 B、 或4 C、 或2 D、 或28. 已知 , , ,则( )A、 B、 C、 D、9. 在 中, 是 的中点, 是 的中点,延长 到 ,使 ,若 , ,则 ( )A、 B、 C、 D、10. 若函数 的最大值是0,最小值是-4,最小正周期是 ,且当 时函数 取得最大值,则函数 的单调递增区间是( )A、 B、 C、 D、11. 已知双曲线 , 分别是双曲线的左右焦点,存在一点 , 点关于 点的对称点是 点, 点关于 点的对称点是 点,线段 的中点在双曲线上,则 ( )A、 B、4 C、 D、812. 四棱锥 中,底面 为矩形, , ,且 ,当该四棱锥的体积最大时,其外接球的表面积为( )
A、 或4 B、 或4 C、 或2 D、 或28. 已知 , , ,则( )A、 B、 C、 D、9. 在 中, 是 的中点, 是 的中点,延长 到 ,使 ,若 , ,则 ( )A、 B、 C、 D、10. 若函数 的最大值是0,最小值是-4,最小正周期是 ,且当 时函数 取得最大值,则函数 的单调递增区间是( )A、 B、 C、 D、11. 已知双曲线 , 分别是双曲线的左右焦点,存在一点 , 点关于 点的对称点是 点, 点关于 点的对称点是 点,线段 的中点在双曲线上,则 ( )A、 B、4 C、 D、812. 四棱锥 中,底面 为矩形, , ,且 ,当该四棱锥的体积最大时,其外接球的表面积为( )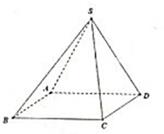 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在某次语文考试中, 、 、 三名同学中只有一名同学优秀,当他们被问到谁得到了优秀时,C说:“ 没有得优秀”; 说:“我得了优秀”; 说:“ 说得是真话”。事实证明:在这三名同学中,只有一人说的是假话,那么得优秀的同学是 .14. , 满足约束条件 ,则目标函数 的最大值 .15. 中, 、 、 角的对边为 、 、 ,其中 ,若 , , ,则 等于 .16. 定义在 上的函数 的导函数为 , .若对任意 ,都有 ,则使得 成立的 的取值范围为.
三、解答题
-
17. 数列 的前 项和 , .(1)、求数列 的通项公式;(2)、设 ,求 的前 项和 .18. 某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据 如下表所示
日期
4月1日
4月2日
4月3日
4月4日
4月5日
4月6日
试销价 元
9
11
10
12
13
14
产品销量 件
40
32
29
35
44
(1)、试根据4月2日、3日、4日的三组数据,求 关于 的线性回归方程 ,并预测4月6日的产品销售量 ;(2)、若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件 的概率.参考公式:
其中 ,
19. 已知如图(1)直角梯形 , , , , , 为 的中点,沿 将梯形 折起(如图2),使 .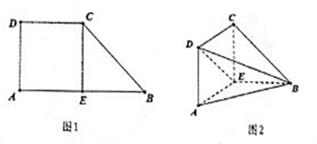 (1)、证明: 平面 ;(2)、求点 到平面 的距离.20. 设椭圆 : 的左顶点为 ,上顶点为 ,已知直线 的斜率为 , .(1)、求椭圆 的方程;(2)、设直线 : 与椭圆 交于不同的两点 、 ,且点 在以 为直径的圆外(其中 为坐标原点),求 的取值范围.
(1)、证明: 平面 ;(2)、求点 到平面 的距离.20. 设椭圆 : 的左顶点为 ,上顶点为 ,已知直线 的斜率为 , .(1)、求椭圆 的方程;(2)、设直线 : 与椭圆 交于不同的两点 、 ,且点 在以 为直径的圆外(其中 为坐标原点),求 的取值范围.