重庆市北碚区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1. 在- ,0,-|-5|,-0.6,2, ,-10中负数的个数有( )A、3 B、4 C、5 D、62. |a|=-a,则a一定是( )A、负数 B、正数 C、零或负数 D、非负数3. 下列运算正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、2a2+3a2=5a6 D、(a+2b)(a﹣2b)=a2﹣4b24. 若a<c<0<b,则下列各式正确的是( )A、abc<0 B、abc=0 C、abc>0 D、无法确定5. 2018年10月24日,被外媒冠以“中国奇迹”之称的“超级工程”港珠澳大桥,正式通车.港珠澳大桥是新中国建设史上里程最长投资最多施工难度最大的跨海桥梁。其中最大沉管隧道排水量超过75000吨。75000用科学记数法表示为( )A、0.75×105 B、75×103 C、7.5×104 D、7.5×1056. 若 是关于x的一元二次方程 的一个解,则 的值是A、17 B、1026 C、2018 D、40537. 如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )
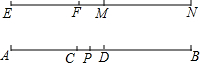 A、4 B、5 C、5.5 D、68. 下列四个图形中,不能推出∠2与∠1相等的是( )A、
A、4 B、5 C、5.5 D、68. 下列四个图形中,不能推出∠2与∠1相等的是( )A、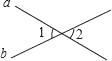 B、
B、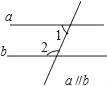 C、
C、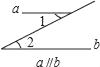 D、
D、 9.
9.如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
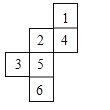 A、7 B、8 C、9 D、1010. 如图,O为直线AB上一点,OM平分∠AOC , ON平分∠BOC , 则图中互余的角有( )
A、7 B、8 C、9 D、1010. 如图,O为直线AB上一点,OM平分∠AOC , ON平分∠BOC , 则图中互余的角有( ) A、4对 B、3对 C、2对 D、1对11. 一个角的余角是它的补角的 ,这个角的补角是( )A、30° B、60° C、120° D、150°12. 如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )
A、4对 B、3对 C、2对 D、1对11. 一个角的余角是它的补角的 ,这个角的补角是( )A、30° B、60° C、120° D、150°12. 如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )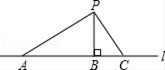 A、②③ B、①②③ C、③④ D、①②③④
A、②③ B、①②③ C、③④ D、①②③④二、填空题
-
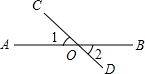
13. 已知|a+1|+|b+3|=0,则a= , b=.14. 若x、y互为相反数,a、b互为倒数,c的绝对值等于2,则 =.15. 观察下列单项式:a,-2a2 , 4a3 , -8a4 , 16a5 , …,按此规律第n个单项式是.(n是正整数)16. 如图,直线AB、CD相交于点O , 若∠1+∠2=100°,则∠BOC等于 .
 17. 用一张长方形纸条折成如图所示图形,如果∠1=130°,那么∠2=.
17. 用一张长方形纸条折成如图所示图形,如果∠1=130°,那么∠2=.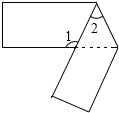 18. 长方形如图折叠,已知∠AEB′=56°,则∠BEF=度.
18. 长方形如图折叠,已知∠AEB′=56°,则∠BEF=度.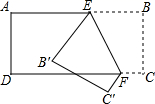
三、解答题
-
19. 计算:(1)、-14- ×[2-(-3)2]÷(-7);(2)、(1 - + )÷(- )-8×(- )3 .20. 如图,已知:BE=CF , AB∥CD , AB=CD . 求证:AF∥DE .
 21. 实数a,b,c在数轴上的位置如图,化简|b+c|-|b+a|+|a+c|.
21. 实数a,b,c在数轴上的位置如图,化简|b+c|-|b+a|+|a+c|. 22.
22.
(1)、已知3x2-5x+1=0,求下列各式的值:①3x+ ;②9x2+ ;
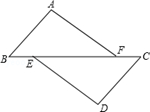
(2)、若3xm+1-2xn-1+xn是关于x的二次多项式,试求3(m-n)2-4(n-m)2-(m-n)3+2(n-m)3的值.23. 已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE.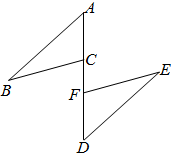
求证:
(1)、△ABC≌△DEF;(2)、BC∥EF.24. 已知如图,直线AB、CD相交于点O,∠COE=90°. (1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.25. 阅读下列材料.
(1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.25. 阅读下列材料.让我们规定一种运算 =ad-cb,如 =2×5-3×4=-2,再如 =4x-2.按照这种运算规定,请解答下列问题.
(1)、计算: ; ; 的值;(2)、当x=-1时,求 的值(要求写出计算过程).26. 如图 问题情境:如图1, , , .求 度数.
问题情境:如图1, , , .求 度数.小明的思路是:如图2,过 作 ,通过平行线性质,可得 .
问题迁移:
(1)、如图3, ,点 在射线 上运动,当点 在 、 两点之间运动时, , . 、 、 之间有何数量关系?请说明理由;(2)、在(1)的条件下,如果点 在 、 两点外侧运动时(点 与点 、 、 三点不重合),请你直接写出 、 、 间的数量关系.