浙江省宁波市象山县2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-04-12 类型：期末考试

进入出卷网下载

一、单选题

1. 我国是最早使用负数的国家，东汉初，在我国著名的数学书 $《$ 九章算术 $》$ 中，明确提出了“正负术” $.$ 如果盈利2000元记作“ $+ 2000$ 元”，那么亏损3000元记作 $($ $)$

A、 $- 3000$ 元 B、3000元 C、5000元 D、 $- 5000$ 元

查看试题解析
2. 64的平方根是 $($ $)$

A、 8 B、4 C、 $\pm 8$ D、 $\pm 4$

查看试题解析
3. 2018年1月，“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发，这标志着“墨子号”具备了洲际量子保密通信的能力 $.$ 数字7600用科学记数法表示为 $($ $)$

A、 $0.76 \times 10^{4}$ B、 $7.6 \times 10^{3}$ C、 $7.6 \times 10^{4}$ D、 $76 \times 10^{2}$

查看试题解析
4. 下列各式运算正确的是 $($ $)$

A、 $3 x + 2 y = 5 xy$ B、 $3 x + 5 x = 8 x^{2}$ C、 $10 x^{2} - 3 x^{2} = 7$ D、 $10 {xy}^{2} - 5 y^{2} x = 5 {xy}^{2}$

查看试题解析
5. 如图为洪涛同学的小测卷，他的得分应是 $($ $)$

A、25分 B、50分 C、75分 D、100分

查看试题解析
6. 下列说法中正确是 $($ $)$

A、 $\frac{π}{3}$ 是分数 B、实数和数轴上的点一一对应 C、 $- \frac{3 ab}{2}$ 的系数为 $- \frac{1}{2}$ D、 $∠ α$ 的余角 $= 180^{\circ} - ∠ α$

查看试题解析
7. 有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（）

A、 $a + b < 0$ B、 $a - b < 0$ C、 $a b > 0$ D、 $\frac{a}{b} > 0$

查看试题解析
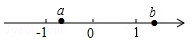8. 已知a，b为两个连续整数，且 $a < \sqrt{13} < b$ ，则 $a + b$ 的值为 $($ $)$

A、9 B、8 C、7 D、6

查看试题解析
9. 定义一种新运算： $a ※ b = {\begin{matrix} a - b (a \geq b) \\ 3 b (a < b) \end{matrix}$ ，则 $2 ※ 3 - 4 ※ 3$ 的值 $($ $)$

A、5 B、8 C、7 D、6

查看试题解析
10. 某同学在解关于x的方程 $5 a - x = 13$ 时，误将 $- x$ 看作 $+ x$ ，得到方程的解为 $x = - 2$ ，则a的值为 $($ $)$

A、3 B、 $\frac{11}{5}$ C、2 D、1

查看试题解析
11. 一列数 $a_{1}$ ， $a_{2}$ ， $a_{3} \dots$ ，其中 $a_{1} = \frac{1}{2}$ ， $a_{2} = \frac{1}{1 - a_{1}}$ ， $a_{3} = \frac{1}{1 - a_{2}}$ ， $\dots \dots$ ， $a_{n} = \frac{1}{1 - a_{n - 1}} (n$ 为不小于2的整数 $)$ ，则 $a_{2018} = ($ $)$

A、 $\frac{1}{2}$ B、2 C、2018 D、 $- 1$

查看试题解析
12. 如图是一张长方形的拼图卡片，它被分割成4个大小不同的正方形和一个长方形，若要计算整张卡片的周长，则只需知道哪个正方形的边长即可 $($ $)$

A、 $④$ B、 $③$ C、 $②$ D、 $①$

查看试题解析

二、填空题

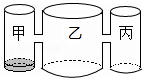
13. 在一面墙上用一根钉子钉木条时，木条总是来回晃动；用两根钉子钉木条时，木条就会固定不动，用数学知识解释这两种生活现象为．

查看试题解析
14. 若 ${(a + 1)}^{2} + | b - 2 | = 0$ ，则 $a + b =$ ．

查看试题解析
15. 已知 $3 b - a = 2$ ，则代数式 $2 a - 6 b - 3$ 的值是．

查看试题解析
16. 在我国著名的数学书 $《$ 九章算术 $》$ 中曾记载这样一个数学问题：“今有共买羊，人出五，不足四十五；人出七，不足三，问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少？设羊价为x钱，则可列关于x的方程为．

查看试题解析
17. 已知线段 $AB = 10 cm$ ，点D是线段AB的中点，直线AB上有一点C，并且 $BC = 2$ cm，则线段 $DC =$ ．

查看试题解析
18. 实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm）．现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升 $\frac{5}{6}$ cm，则开始注入分钟的水量后，甲与乙的水位高度之差是0.5cm．

查看试题解析

三、解答题

19. 计算

(1)、 $| - 2 | + \sqrt{\frac{1}{4}} + {(- 1)}^{2018}$

(2)、 $- 2^{2} - 24 \times (\frac{1}{12} - \frac{5}{6} + \frac{3}{8})$

查看试题解析
20. 解方程：

(1)、 $2 - 3 (x - 5) = 2 x$

(2)、 $\frac{3 x - 1}{3} = 1 - \frac{4 x - 1}{6}$

查看试题解析
21. 为提高市民的环保意识，倡导“节能减排，绿色出行”，某市计划在城区投放一批“共享单车”这批单车分为A，B两种不同款型，其中A型车单价400元，B型车单价320元．

(1)、今年年初，“共享单车”试点投放在某市中心城区正式启动．投放A，B两种款型的单车共100辆，总价值36800元．试问本次试点投放的A型车与B型车各多少辆？

(2)、试点投放活动得到了广大市民的认可，该市决定将此项公益活动在整个城区全面铺开．按照试点投放中A，B两车型的数量比进行投放，且投资总价值不低于184万元．请问城区10万人口平均每100人至少享有A型车与B型车各多少辆？

查看试题解析
22. 先化简，再求值： $3 (1 - \frac{1}{3} a) - 2 (\frac{1}{2} a^{2} + 4 a - 2)$ ，其中 $a = - 2$

查看试题解析
23. 某幼儿园举行用火柴棒摆“金鱼”比赛如图所示，请仔细观察并找出规律，解答下列

问题：

(1)、按照此规律，摆第10个图时，需根火柴棒；摆第n个图时所需根火柴棒；

(2)、用1202根火柴棒能按此规律摆出一个“金鱼”图案吗？若能，说明是第几个图形；若不能，请说明理由．

查看试题解析
24. 如图，直线AB、CD相交于点O，已知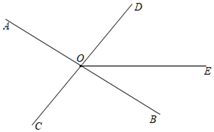 $∠ AOC = 80^{\circ}$ ，OE把 $∠ BOD$ 分成两个角，且 $∠ BOE$ ： $∠ EOD = 2$ ：3

(1)、求 $∠ EOB$ 的度数；

(2)、过点O作射线 $OF ⊥ OE$ ，求 $∠ DOF$ 的度数．

查看试题解析
25. 如图所示，已知A，B是数轴上的两点 $($ 点A在点B左边 $)$ ，O为原点，且OA： $OB = 1$ ：5， $AB = 180.$ 现有点P从点A出发向右运动，与此同时点Q从点B出发向左运动，经过30秒后，P、Q在点D处相遇 $.$ 相遇后，两点继续沿之前方向运动，点Q到达点A后立刻按原速向右运动，当点Q返回到点B时，P、Q两点立即停止运动，若点Q的速度是点P的3倍，设运动的时间为t秒，请回答下列问题：

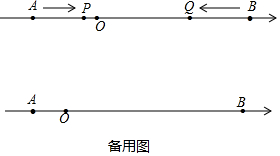(1)、点A表示的数为；

(2)、求点D表示的数是多少；

(3)、t为何值时，点Q在返途中追上点P？

查看试题解析