江苏省无锡市江阴市2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期：2019-04-12 类型：期末考试
一、单选题
-
1. ﹣3的相反数是（ ）A、﹣3 B、3 C、- D、2. 下列计算正确的是（ ）A、x－2x=－x B、2x－y=xy C、x2+x2=x4 D、5y－3y=23. 已知2xmy2和－ x3yn是同类项，那么m+n的值是（ ）A、2 B、4 C、6 D、54. 方程2x－1＝3x＋2的解为 （ ）A、x＝1 B、x＝－1 C、x＝－3 D、x＝35. 已知a + b =3，b − c = 12，则a + 2b − c的值为（ ）A、15 B、9 C、−15 D、−96.
如图，甲从A点出发向北偏东70°方向走到点B，乙从点A出发向南偏西15°方向走到点C，则∠BAC的度数是（ ）
A、85° B、160° C、125° D、105°7. 一个几何体的表面展开图如图所示，则这个几何体是（ ）
A、四棱锥 B、四棱柱 C、三棱锥 D、三棱柱8. 已知a＝5，│b│＝8，且满足a＋b＜0，则a－b的值为（ ）A、3 B、－3 C、－13 D、139. 给出下列说法：①棱柱的上、下底面的形状相同；②相等的角是对顶角；③若AB=BC，则点B为线段AC的中点；④直线外一点与直线上各点连接的所有线段中，垂线段最短．其中正确说法的个数有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，有一些点组成形如四边形的图案，每条“边”（包括顶点）有n（n>1）个点．当n＝2019时，这个图形总的点数S为（ ）
A、8067 B、8068 C、8072 D、8076二、填空题
-
11. -7的倒数是 .
12. 多项式2x2 ＋6x2y－3xy3的次数是次．13. 四边形的内角和为 ．14. 今年“五一”节日期间，我市四个旅游景区共接待游客约303000多人次，这个数据用科学记数法可记为 ．15. 68°30′的补角为 ．16. 已知直线l上有A、B、C三点，且AB=8cm，BC=3cm，则线段AC=cm．17. 如图，若开始输入的x的值为 ，按所示的程序运算，最后输出的结果为 ．
18. 如图，将三个相同正方形的一个顶点重合放置，且∠COE=40°，∠BOF=30°，则∠AOD=°．
三、解答题
-
19. 计算：(1)、(2)、 ÷ ．20. 解方程：(1)、4－3（2－x）＝5x(2)、 ．21. 先化简，再求值：－5x2y－[2x2y－3(xy－2x2y)]＋2xy，其中x＝－1，y＝－2．22. 如图是由10个同样大小的小正方体搭成的物体，(1)、请分别画出它的主视图和俯视图．(2)、在主视图和俯视图不变的情况下，你认为最多还可以添加个小正方体．
23. 如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．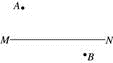
(1)、在直线MN上取一点C，使线段AC最短．依据是 ．(2)、在直线MN上取一点D，使线段AD＋BD最短．依据是 ．24. 如图，直线AB、CD相交于点O，∠AOD＝120°，FO⊥OD，OE平分∠BOD．
(1)、求∠EOF的度数；(2)、试说明OB平分∠EOF．25. 某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个，这两种玻璃保温杯的进价、标价如表所示：
(1)、这两种玻璃保温杯各购进多少个?(2)、若A型玻璃保温杯按标价的9折出售，B型玻璃保温杯按标价的8.5折出售，且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏，不能进行销售，请问这批玻璃保温杯全部售出后，该家居专营店共获利多少元?26. 已知关于m的方程 (m－16)＝－5的解也是关于x的方程2 (x－3)－n＝3的解．(1)、求m、n的值；(2)、已知线段AB＝m，在射线AB上取一点P，恰好使 ＝n，点Q为线段PB的中点，求AQ的长．
27. 在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）.12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．
(1)、求OC的长；(2)、经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；(3)、若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．