江苏省无锡市惠山区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-04-12 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、3 B、 $\frac{1}{3}$ C、﹣3 D、 $- \frac{1}{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $5 y - 3 y = 2$ C、 $7 a + a = 7 a^{2}$ D、 $3 x^{2} y - 2 y x^{2} = x^{2} y$

查看试题解析
3. 下列各数：3.14，﹣2，0.131131113，0，﹣π， $\frac{1}{7}$ ， $0. \overset{\cdot}{6}$ ，其中无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 已知 $x = - 1$ 是方程 $2 x - 5 = x + m$ 的解，则m的值是（）

A、﹣4 B、﹣6 C、﹣7 D、﹣8

查看试题解析
5. 有理数 $a$ ， $b$ 在数轴上对应点的位置如图所示，下列各式正确的是（）

A、 $a + b < 0$ B、 $| a | > | b |$ C、 $a - b < 0$ D、 $a b > 0$

查看试题解析
6. 下列说法错误的是（）

A、对顶角相等 B、两点之间所有连线中，线段最短 C、等角的补角相等 D、过任意一点P，都能画一条直线与已知直线平行

查看试题解析
7. 一件毛衣先按成本提高50%标价，再以8折出售，获利28元，求这件毛衣的成本是多少元，若设成本是x元，可列方程为（）

A、0.8x+28=（1+50%）x B、0.8x﹣28=（1+50%）x C、x+28=0.8×（1+50%）x D、x﹣28=0.8×（1+50%）x

查看试题解析
8. 如图，将长方形ABCD沿线段OG折叠到OB'C'G的位置，∠OGC'等于100°，则∠DGC'的度数为（）

A、20° B、25° C、30° D、40°

查看试题解析
9. 把图1所示的正方体的展开图围成正方体（文字露在外面），再将这个正方体按照图2，依次翻滚到第1格，第2格，第3格，第4格，此时正方体朝上一面的文字为（）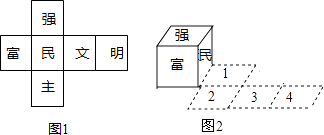

A、富 B、强 C、文 D、民

查看试题解析
10. 如图，电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动，电子蚂蚁P从点A出发，以 $\frac{3}{2}$ 个单位长度/秒的速度绕正方形作顺时针运动，电子蚂蚁Q从点A出发，以 $\frac{1}{2}$ 个单位长度/秒的速度绕正方形作逆时针运动，则它们第2018次相遇在（）

A、点A B、点B C、点C D、点D

查看试题解析

二、填空题

11. 单项式﹣x³y的系数是．

查看试题解析
12. 若代数式2a^mb⁴与-5a²bⁿ⁺¹是同类项，则 $m n$ = ．

查看试题解析
13. 若∠α=54°12'，则∠α的补角是．

查看试题解析
14. 据报道，2018年我市城镇非私营单位就业人员年平均工资超过70500元，将数70500用科学记数法表示为．

查看试题解析
15. 若a²﹣3b=4，则1﹣2a²+6b= ．

查看试题解析
16. 如图，数轴上点A表示的数为a，化简：|a﹣3|﹣2|a+1|= ．（用含a的代数式表示）

查看试题解析
17. 如图，若开始输入的x的值为正整数，最后输出的结果为144，则满足条件的 $x$ 的值为．

查看试题解析
18. 如图，已知点A是射线BE上一点，过A作AC⊥BF，垂足为C，CD⊥BE，垂足为D．给出下列结论：①∠1是∠ACD的余角；②图中互余的角共有3对；③∠1的补角只有∠DCF；④与∠ADC互补的角共有3个．其中正确结论有．

查看试题解析

三、解答题

19. 计算：

(1)、 $(\frac{1}{4} - \frac{5}{6} + \frac{2}{3}) \times (- 24)$

(2)、 $- 1^{2019} + {(- 2)}^{2} \div \frac{4}{5} + | 1 - 2^{2} |$

查看试题解析
20. 解方程：

(1)、 $3 (2 - x) = 4 - x$

(2)、 $\frac{x + 1}{2} - 1 = \frac{3 x - 2}{3}$

查看试题解析
21. 先化简，后求值：（3a²﹣4ab）﹣2（a²+2ab），其中a，b满足|a+1|+（2﹣b）²=0．

查看试题解析
22. 在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．已知三角形ABC的三个顶点都在格点上．

(1)、按下列要求画图：过点B和一格点D画AC的平行线BD，过点C和一格点E画BC的垂线CE，并在图中标出格点D和E；

(2)、求三角形ABC的面积．

查看试题解析
23. 如图，是由8个大小相同的小正方体组合成的简单几何体．

(1)、该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；

(2)、如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的俯视图和主视图不变，那么请画出添加小正方体后所得几何体可能的左视图．

查看试题解析
24. 如图，直线AB、CD相交于点O．已知∠BOD＝75°，OE把∠AOC分成两个角，且∠AOE：∠EOC＝2：3．

(1)、求∠AOE的度数；

(2)、若OF平分∠BOE，问：OB是∠DOF的平分线吗？试说明理由．

查看试题解析
25. 某服装店计划从批发市场购进甲、乙两种不同款式的服装共80件进行销售．已知每件甲款服装的价格比每件乙款服装的价格贵10元，购买30件甲款服装的费用比购买35件乙款服装的费用少100元．

(1)、求购进甲、乙两种款式的服装每件的价格各是多少元？

(2)、若该服装店购进乙款服装的件数是甲款服装件数的3倍，并都以每件120元的价格进行销售．经过一段时间，甲款服装全部售完，乙款服装还余20件未售完，该店决定对余下服装打8折销售．求该店把这批服装全部售完获得的利润．

查看试题解析
26. 如图，直线l上有A、B两点，点O是线段AB上的一点，且OA=10cm，OB=5cm．

(1)、若点C是线段 AB 的中点，求线段CO的长．

(2)、若动点 P、Q 分别从 A、B 同时出发，向右运动，点P的速度为4cm/s，点Q的速度为3cm/s，设运动时间为 x 秒，
①当 x=秒时，PQ=1cm；
②若点M从点O以7cm/s的速度与P、Q两点同时向右运动，是否存在常数m，使得4PM+3OQ﹣mOM为定值，若存在请求出m值以及这个定值；若不存在，请说明理由．

(3)、若有两条射线 OC、OD 均从射线OA同时绕点O顺时针方向旋转，OC旋转的速度为6度/秒，OD 旋转的速度为2度/秒.当OC与OD第一次重合时，OC、OD 同时停止旋转，设旋转时间为t秒，当t为何值时，射线 OC⊥OD？

查看试题解析