江苏省南通市港闸区统考2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-04-12 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的相反数是（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
2. 下列运算正确的是（）

A、2a+6b＝8ab B、4x²y﹣5xy²＝﹣x²y C、a²b﹣3ba²＝﹣2a²b D、﹣（﹣a﹣b）＝a﹣b

查看试题解析
3. 数字25800000用科学记数法表示为（）

A、258×10⁵ B、2.58×10⁹ C、2.58×10⁷ D、0.258×10⁸

查看试题解析
4. 单项式 $- \frac{3 x^{2} y}{5}$ 的系数和次数分别是（）

A、﹣3，2 B、﹣3，3 C、 $- \frac{3}{5}$ ，2 D、 $- \frac{3}{5}$ ，3

查看试题解析
5. 如图，已知AB∥CD∥EF，FC平分∠AFE，∠A＝50°，则∠C的度数是（）

A、50° B、45° C、35° D、25°

查看试题解析
6.
如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（　　）

A、2 B、3 C、5 D、7

查看试题解析
7. 下列平面图形中不能围成正方体的是（）

A、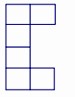 B、 C、 D、

查看试题解析
8. 对于有理数a、b，如果ab＜0，a+b＜0．则下列各式成立的是（　　）

A、a＜0，b＜0 B、a＞0，b＜0且|b|＜a C、a＜0，b＞0且|a|＜b D、a＞0，b＜0且|b|＞a

查看试题解析
9. 已知关于x的一次方程（3a+4b）x+1＝0无解，则ab的值为（）

A、正数 B、非正数 C、负数 D、非负数

查看试题解析
10. 某公司员工分别住在A，B，C三个住宅区，A区有25人，B区有15人，C区有10人，三个区在一条直线上，位置如图所示，公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应设在（）

A、A区 B、B区 C、A区或B区 D、C区

查看试题解析

二、填空题

11. 计算：|﹣2|= ．

查看试题解析
12. 计算：－2²⁰¹⁷×（－0.5）²⁰¹⁸ ．

查看试题解析
13. 下列有四个生活、生产现象：①有两个钉子就可以把木条固定在墙上；②从A地到B地架设电线，总是尽可能沿着线段AB架设；③植树时，只要定出两棵树的位置，就能确定同一行所在的直线；④把弯曲的公路改直，就能缩短路程．其中可用基本事实“两点之间，线段最短”来解释的现象有（填序号）．

查看试题解析
14. 一个角的补角比它的余角的2倍还多20°,这个角的度数为.

查看试题解析
15. 已知关于x的方程 $\frac{x}{2} + \frac{m}{3}$ ＝x﹣4与方程2x+5＝3（x﹣1）的解相同，则m＝．

查看试题解析
16. 计算：21°15′×5 ＝°．

查看试题解析
17. 若|a+1|+|a﹣2|＝5，|b﹣2|+|b+3|＝7，则a+b＝．

查看试题解析
18. 如图，按下列程序进行计算，经过三次输入，最后输出的数是12，则最初输入的数是 .

查看试题解析

三、解答题

19. 计算：

(1)、1﹣4+3﹣0.5

(2)、18+32÷（﹣2）³﹣（﹣4）²×5

查看试题解析
20. 化简：

(1)、（2a﹣b）﹣（2b﹣3a）﹣2（a﹣2b）

(2)、2x²﹣[7x﹣（4x﹣3）﹣x²]

查看试题解析
21. 解下列方程：

(1)、2（x+3）＝5x

(2)、 $\frac{y + 1}{2} - 1 = 2 + \frac{2 - y}{4}$

查看试题解析
22. 如图是由10个同样大小的小正方体搭成的物体，

(1)、请分别画出它的主视图和俯视图．

(2)、在主视图和俯视图不变的情况下，你认为最多还可以添加个小正方体．

查看试题解析
23. 根据要求画图，并回答问题．
已知：直线AB，CD相交于点O，且OE⊥AB．

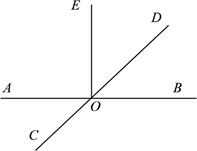(1)、过点O画直线MN⊥CD；

(2)、若点F是（1）中所画直线MN上任意一点(O点除外)，若∠AOC＝35°，求∠EOF的度数．

查看试题解析
24. 已知当x＝2，y＝－4时，ax³+ $\frac{1}{2}$ by+8=2018 ，求当x＝－4，y＝ $- \frac{1}{2}$ 时，式子3ax－24by³+6的值．

查看试题解析
25. 点 O 是直线 AB上一点，∠COD 是直角，OE平分∠BOC．

(1)、①如图1，若∠DOE＝25°，求∠AOC 的度数；
②如图2，若∠DOE＝α，直接写出∠AOC的度数（用含α的式子表示）；

(2)、将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置．探究∠DOE 与∠AOC 的度数之间的关系，写出你的结论，并说明理由．

查看试题解析
26. 某超市对顾客实行优惠购物，规定如下：
（1）若一次性购物不超过100元，则不予优惠；
（2）若一次性购物超过100元，但不超过300元，按标价给予九折优惠；
（3）若一次性购物超过300元，其中300元以下部分（包括300元）给予九折优惠；超过300元部分给予八折优惠.
小李两次去该超市购物，分别付款99元和252元.现在小张决定一次性购买小李分两次购买的物品，他需付款多少元?

查看试题解析
27. 如图，点D，点E分别在三角形ABC的边上，已知∠AED＝∠ACB， DF，BE分别平分∠ADE，∠ABC，那么∠FDE与∠DEB相等吗？请说明理由．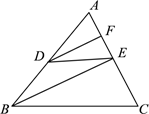

查看试题解析
28. 已知数轴上两点A，B对应的数分别为﹣4，8．

(1)、如图1，如果点P和点Q分别从点A，B同时出发，沿数轴负方向运动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒6个单位．
①A，B两点之间的距离为．

②当P，Q两点相遇时，点P在数轴上对应的数是．

③求点P出发多少秒后，与点Q之间相距4个单位长度？

(2)、如图2，如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动，点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动，点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动，若三个点同时出发，经过多少秒后有MP＝MQ？

查看试题解析