重庆市綦江区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-04-12 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $(x - 2) (x + 3) = 0$ 的根是（）

A、 $x_{1} = 2, x_{2} = - 3$ B、 $x_{1} = - 2, x_{2} = - 3$ C、 $x_{1} = 2, x_{2} = 3$ D、 $x_{1} = - 2, x_{2} = 3$

查看试题解析
2. 在平面直角坐标系中，抛物线y=- $\frac{1}{2}$ （x+1）²- $\frac{1}{2}$ 的顶点是（）

A、（-1，- $\frac{1}{2}$ ） B、（-1， $\frac{1}{2}$ ） C、（1，- $\frac{1}{2}$ ） D、（1， $\frac{1}{2}$ ）

查看试题解析
3. 点A（－5，2)关于原点O对称的点为B，则点B的坐标是（）

A、（－5，－2） B、（5，－2） C、（－5，2） D、（5，2）

查看试题解析
4. 如图，⊙O的弦AB等于它的半径，点C在优弧AB上，则（）

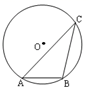A、∠ACB＝28° B、∠CAB＝70° C、∠ABC＝110° D、∠ACB＝30°

查看试题解析
5. 下列交通标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 若六边形的边心距为 $\sqrt{3}$ ，则这个正六边形的周长为（）

A、6 B、9 C、12 D、18

查看试题解析
7. 已知方程 $x^{2} - 3 x - k = 0$ 的一个根为—2，那么它的另一个根为（）

A、5 B、1 C、3 D、—2

查看试题解析
8. 同时投掷两个骰子，点数的和大于10的概率为（）

A、 $\frac{1}{16}$ B、 $\frac{1}{12}$ C、 $\frac{1}{8}$ D、 $\frac{1}{4}$

查看试题解析
9. 如图，点 $A$ ， $B$ 是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上的两点，过点 $A$ ， $B$ 分别作 $A C ⊥ x$ 轴于点 $C$ ， $B D ⊥ x$ 轴于点 $D$ ，连接 $O A$ 、 $B C$ ，已知点 $C (2 ， 0)$ ， $B D = 3$ ， $S_{Δ B C D} = 3$ ，则 $S_{Δ A O C}$ 为 $($ $)$

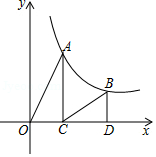A、2 B、3 C、4 D、6

查看试题解析
10. 如图，在⊙O中，直径AB垂直弦CD，E为BC弧上一点，下列结论：①∠1=∠2；②∠3=2∠4；③∠3+∠5=180°，其中正确的是（）

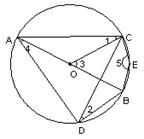A、①③ B、②③ C、①②③ D、①②

查看试题解析
11. 已知反比例函数 $y = \frac{k^{2} + 4 k + 5}{x}$ 图象上有三点 $A (x_{1}$ ， $y_{1})$ ， $B (x_{2}$ ， $y_{2})$ ， $C (x_{3}$ ， $y_{3})$ 且 $x_{1} > x_{2} > 0 > x_{3}$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为 $($ $)$

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
12. 已知二次函数 y=ax²+bx+c（a≠0）的图象如图，有下列 5 个结论：①4a+2b+c＞0；②abc＜0；③b＜a+c；④3b＞2c；⑤a+b＜m（am+b），（m≠1 的实数）；其中正确结论的个数为（）

A、2 个 B、3 个 C、4 个 D、5 个

查看试题解析

二、填空题

13. 如果将抛物线 $y = x^{2} + 2$ 向下平移1个单位，那么所得新抛物线的解析式为．

查看试题解析
14. 如图所示，宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm）则该圆的半径为cm．

查看试题解析
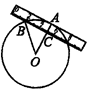15. 含有4种花色36张扑克牌的牌面都朝下，每次抽出一张记下花色后再原样放回，洗匀牌后再抽，不断重复上述过程，记录抽到红心的频率为25%，那么扑克牌花色是红心的大约有张．

查看试题解析
16. 如图，在 $x$ 轴的正半轴上依次截取 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = A_{3} A_{4} = A_{4} A_{5}$ ……，过点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 、 $A_{4}$ 、 $A_{5}$ ……，分别作 $x$ 轴的垂线与反比例函数 $y = \frac{2}{x} (x \neq 0)$ 的图象相交于点 $P_{1}$ 、 $P_{2}$ 、 $P_{3}$ 、 $P_{4}$ 、 $P_{5}$ ……，得直角三角形 $O P_{1} A_{1}$ 、 $A_{1} P_{2} A_{2}$ ， $A_{2} P_{3} A_{3}$ ， $A_{3} P_{4} A_{4}$ ， $A_{4} P_{5} A_{5}$ ……，并设其面积分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 、 $S_{4}$ 、 $S_{5}$ ……，则 $S_{10} =$ ． $(n ⩾ 1$ 的整数）.

查看试题解析
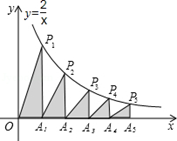17. 如图，扇形AOB的圆心角是为90°，四边形OCDE是边长为1的正方形，点C，E，D 分别在OA，OB， $\overset{⌢}{A B}$ 上，过A作AF⊥ED交ED的延长线于点F，那么图中阴影部分的面积为．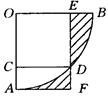

查看试题解析

三、解答题

18. 如图，张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为 $1$ 米的正方形后，剩下的部分刚好能围成一个容积为 $15 m^{3}$ 的无盖长方体箱子，且此长方体箱子的底面长比宽多 $2$ 米，现已知购买这种铁皮每平方米需 $20$ 元钱，问张大叔购回这张矩形铁皮共花了多少元钱？

查看试题解析
19. 解方程：

(1)、 $x^{2} - 8 x - 1 = 0$ ;

(2)、 ${(x - 2)}^{2} - 6 (x - 2) + 8 = 0$

查看试题解析
20. 在我区电视台举行的“讲故事”比赛中，甲、乙、丙三位评委，对选手的综合表现，分别给出“待定”或“通过” 的结论．

(1)、利用树状图写出三位评委给出选手A的所有可能的结论；

(2)、对于选手A，只有甲、乙两位评委给出相同结论的概率是多少？

查看试题解析
21. 如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过O作OH⊥AC于点H．若OH＝3，AB＝8，BO＝10．求：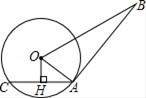

(1)、⊙O的半径；

(2)、弦AC的长(结果保留根号)．

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} - 2 (m + 1) x + m^{2} = 0$ ．

(1)、当 $m$ 取何值时，方程有两个不相等的实数根．

(2)、为 $m$ 选取一个合适的整数，使方程有两个不相等的实数根，并求这两个根．

查看试题解析
23. 已知网格上最小的正方形的边长为1，如图所示建立直角坐标系.

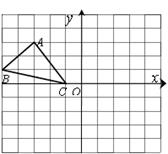(1)、分别写出A、B、C三点的坐标；

(2)、作△ABC关于原点O的对称图形△ $A^{'} B^{'} C^{'}$ （不写作法）；

(3)、求△ABC的面积．

查看试题解析
24. 如图，反比例函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = x - 2$ 的图象交于点 $A (a ， 2)$ 和点B，连接OA，OB.

(1)、求反比例函数的解析式和点B的坐标；

(2)、求 $Δ A O B$ 的面积；

(3)、观察图象，直接写出满足 $y_{1} > y_{2}$ 的实数x的取值范围．

查看试题解析
25. 阅读题.
材料一：若一个整数m能表示成a²-b²(a，b为整数)的形式，则称这个数为“完美数”.例如，3=2²-1² ， 9=3²-0² ， 12=4²-2² ，则3，9，12都是“完美数”；再如，M=x²+2xy=(x+y)²-y² ， (x，y是整数)，所以M也是”完美数”.

材料二：任何一个正整数n都可以进行这样的分解：n＝p×q(p、q是正整数，且p≤q)．如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并且规定F(n)＝ $\frac{p}{q}$ .例如18＝1×18＝2×9＝3×6，这三种分解中3和6的差的绝对值最小，所以就有F(18)＝ $\frac{3}{6} = \frac{1}{2}$ .请解答下列问题：

(1)、8（填写“是”或“不是”）一个完美数，F(8)= .

(2)、如果m和n都是”完美数”，试说明mn也是完美数”.

(3)、若一个两位数n的十位数和个位数分别为x，y(1≤x≤9)，n为“完美数”且x+y能够被8整除，求F(n)的最大值.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + 2 x - 3$ 与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点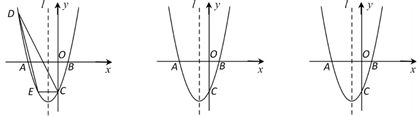 $C$ ．对称轴为直线 $l$ ，点 $D (- 4 ， n)$ 在抛物线上．

(1)、求直线 $C D$ 的解析式；

(2)、 $E$ 为直线 $C D$ 下方抛物线上的一点，连接 $E C$ 、 $E D$ ．当 $Δ E C D$ 的面积最大时，在直线 $l$ 上取一点 $M$ ，过 $M$ 作 $y$ 轴的垂线，垂足为点 $N$ ，连接 $E M$ 、 $B N$ ．若 $E M = B N$ 时，求 $E M + M N + B N$ 的值；

(3)、将抛物线 $y = x^{2} + 2 x - 3$ 沿 $x$ 轴正方向平移得到新抛物线 $y^{'}$ ， $y^{'}$ 经过原点 $O$ ． $y^{'}$ 与 $x$ 轴的另一个交点为 $F$ ．设 $P$ 是抛物线 $y^{'}$ 上任意一点，点 $Q$ 在直线 $l$ 上， $Δ P F Q$ 能否成为以点 $P$ 为直角顶点的等腰直角三角形？若能，直接写出点 $P$ 的坐标．若不能，请说明理由．

查看试题解析