浙江省湖州市吴兴区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1. 已知两个相似三角形的对应边之比为1:3,则它们的周长比为( )A、1:9 B、9:1 C、1:6 D、1:32. 下列事件中,属于必然事件的是( )A、掷一枚硬币,正面朝上 B、三角形任意两边之差小于第三边 C、一个三角形三个内角之和大于180° D、在只有红球的盒子里摸到白球3. 将抛物线y=2x2向右平移3个单位,能得到的抛物线是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x+3)2 D、y=2(x﹣3)24. 已知圆心角为60°的扇形面积为24π,那么扇形的半径为( )A、12 B、6 C、 D、5. 如图,直线 ,直线 分别与 相交于点 和点 若 则 等于( )
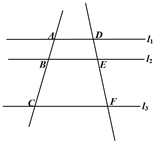 A、6 B、8 C、9 D、126. 如图,已知Rt△ABC中,∠C=90°,AC=6,tanA= ,则AB的长是( )
A、6 B、8 C、9 D、126. 如图,已知Rt△ABC中,∠C=90°,AC=6,tanA= ,则AB的长是( )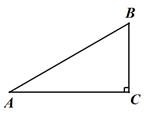 A、 B、 C、12 D、67. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度是( )
A、 B、 C、12 D、67. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度是( )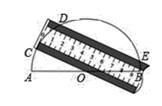 A、4cm B、3cm C、2cm D、1cm8. 已知(1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=﹣x2﹣4x+m上的点,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y1<y3<y29. 如图,在6×8的正方形网格中,共有48个边长为1 的小正方形.A,B,C,D,E都是正方形网格上的格点.连接DE,DB交AC于点P、Q,则PQ的值是( )
A、4cm B、3cm C、2cm D、1cm8. 已知(1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=﹣x2﹣4x+m上的点,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y1<y3<y29. 如图,在6×8的正方形网格中,共有48个边长为1 的小正方形.A,B,C,D,E都是正方形网格上的格点.连接DE,DB交AC于点P、Q,则PQ的值是( )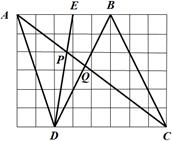 A、 B、 C、 D、10. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A、 B、 C、 D、10. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )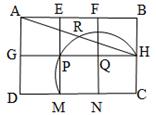 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 = ,则 =.12. 抛物线y=(x-2)2+3的顶点坐标是.13. 一个不透明的口袋中有除颜色外完全相同的5个小球.其中黄球有2个,红球有2个,蓝球有1个,随机摸出一个小球为红球的概率是 .14. 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边AB上的高线,以点C为圆心,2.5为半径作圆,则点D在圆(填“外”,“内”,“上”).
 15. ⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为 ,M是圆上一点,∠BMO=150°.则圆心C的坐标为 .
15. ⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为 ,M是圆上一点,∠BMO=150°.则圆心C的坐标为 .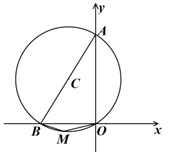
三、解答题
-
16. 如图,一组抛物线的顶点A1(x1 , y1),A2(x2 , y2),…An(xn , yn)(n为正整数)依次是反比例函数 图象上的点,第一条抛物线以A1(x1 , y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2 , y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn , yn)为顶点且经过点Bn-1(2n-2,0),Bn(2n,0),等腰△AnBn-1Bn为第n个三角形.
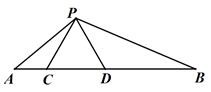
 (1)、写出满足△AnBn-1Bn的面积为整数的n的值.(2)、若第n条抛物线为y=anx2+bnx+cn满足10an+5bn+cn=0,称“滑翔抛物线”,试求出满足条件的“滑翔抛物线”解析式为.17. 计算:4sin45°+3tan230°- .18. 已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.
(1)、写出满足△AnBn-1Bn的面积为整数的n的值.(2)、若第n条抛物线为y=anx2+bnx+cn满足10an+5bn+cn=0,称“滑翔抛物线”,试求出满足条件的“滑翔抛物线”解析式为.17. 计算:4sin45°+3tan230°- .18. 已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.求证:△ACP∽△PDB.
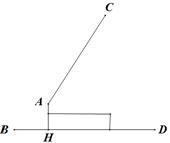
 19. 每年11月9日为消防宣传日,今年“119”消防宣传月活动的主题是“全民参与,防治火灾”.为响应该主题,吴兴区消防大队到某中学进行消防演习.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为5.2m.当起重臂AC长度为16m,张角∠HAC为130°时,求操作平台C离地面的高度(结果精确到0.1m)
19. 每年11月9日为消防宣传日,今年“119”消防宣传月活动的主题是“全民参与,防治火灾”.为响应该主题,吴兴区消防大队到某中学进行消防演习.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为5.2m.当起重臂AC长度为16m,张角∠HAC为130°时,求操作平台C离地面的高度(结果精确到0.1m)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

 20. 近年来,吴兴区坚定不移地践行“绿水青山就是金山银山”发展理念,跑出了乡村旅游发展的“吴兴速度”.已成功打造了汇聚文化体验、乡村休闲、养生养老等多元业态的西塞山省级旅游度假区,拥有A-菰城景区;B-原乡小镇;C-丝绸小镇·西山漾;D-台湾风情小镇;E-古梅花观等高品质景区.吴兴区某中学九年级开展了“我最喜爱的旅游景区”的抽样调查(每人只能选一项).根据收集的数据绘制了两幅不完整的统计图,其中B对应的圆心角为900.请根据图中信息解答下列问题:
20. 近年来,吴兴区坚定不移地践行“绿水青山就是金山银山”发展理念,跑出了乡村旅游发展的“吴兴速度”.已成功打造了汇聚文化体验、乡村休闲、养生养老等多元业态的西塞山省级旅游度假区,拥有A-菰城景区;B-原乡小镇;C-丝绸小镇·西山漾;D-台湾风情小镇;E-古梅花观等高品质景区.吴兴区某中学九年级开展了“我最喜爱的旅游景区”的抽样调查(每人只能选一项).根据收集的数据绘制了两幅不完整的统计图,其中B对应的圆心角为900.请根据图中信息解答下列问题: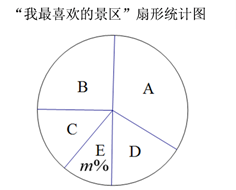
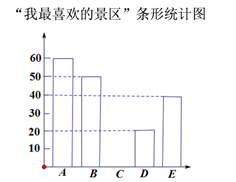 (1)、此次抽取的九年级学生共多少人,m等于多少,并补全条形统计图;(2)、九年级准备在最喜爱原乡小镇的4名优秀学生中任意选择两人去实地考察,这4名学生中有2名男生和2名女生,用树状图或列表法求选出的两名学生都是男生的概率.21. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)、此次抽取的九年级学生共多少人,m等于多少,并补全条形统计图;(2)、九年级准备在最喜爱原乡小镇的4名优秀学生中任意选择两人去实地考察,这4名学生中有2名男生和2名女生,用树状图或列表法求选出的两名学生都是男生的概率.21. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.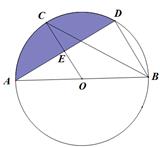 (1)、求证:AE=ED;(2)、若AB=8,∠CBD=30°,求图中阴影部分的面积.22. 吴兴区文体中心,位于湖州市吴兴区东部新城,于今年上半年完全竣工,现已投入使用.其中体育馆可容纳四千人同时观看比赛.现C区有座位400个,某赛事试营销阶段发现:当票价为80元时,可售出C区票280张,若每降价1元,可多售出6张票. 设降价x元(x取正整数)时,可售出观赛座位票y张.
(1)、求证:AE=ED;(2)、若AB=8,∠CBD=30°,求图中阴影部分的面积.22. 吴兴区文体中心,位于湖州市吴兴区东部新城,于今年上半年完全竣工,现已投入使用.其中体育馆可容纳四千人同时观看比赛.现C区有座位400个,某赛事试营销阶段发现:当票价为80元时,可售出C区票280张,若每降价1元,可多售出6张票. 设降价x元(x取正整数)时,可售出观赛座位票y张. (1)、求出y关于x的函数关系式;(2)、设C区的总票价为W元,求W关于x的函数关系式,并求出W的最大值;(3)、求当票价为多少元时,C区的总共售票收入为23800元.23. 如图,在平面直角坐标系中,抛物线 交 轴于 两点,交 轴于点 ,顶点为 ,抛物线对称轴与 轴交点为 .
(1)、求出y关于x的函数关系式;(2)、设C区的总票价为W元,求W关于x的函数关系式,并求出W的最大值;(3)、求当票价为多少元时,C区的总共售票收入为23800元.23. 如图,在平面直角坐标系中,抛物线 交 轴于 两点,交 轴于点 ,顶点为 ,抛物线对称轴与 轴交点为 .
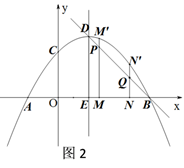 (1)、求直线 的解析式.(2)、点 , 为 轴上两点,其中 , 分别垂直于 轴交抛物线于 ,交直线 于点 .试求:当 为何值时, 的值最大.
(1)、求直线 的解析式.(2)、点 , 为 轴上两点,其中 , 分别垂直于 轴交抛物线于 ,交直线 于点 .试求:当 为何值时, 的值最大.