江苏省无锡市惠山区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、(1,2) B、(1,-2) C、(-1,2) D、(-1,-2)2. 一元二次方程x2=2x的根是 ( )A、x=2 B、x=0 C、x1=0, x2=2 D、x1=0, x2=-23. 已知点A在半径为r的⊙O内,点A与点O的距离为6,则r的取值范围是 ( )A、r < 6 B、r > 6 C、r ≥ 6 D、r ≤ 64. 在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )A、7sin35° B、 C、7cos35° D、7tan35°5. 在比例尺是1:8000的南京市城区地图上,太平南路的长度约为25cm,它的实际长度约为( )
A、320cm B、320m C、2000cm D、2000m6. 如图,点A、B、C均在⊙O上,若∠ABC=40°,则∠AOC的大小是( )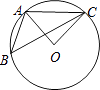 A、90° B、80° C、70° D、50°7. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A、90° B、80° C、70° D、50°7. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( ) A、AB=24m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:28. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A、AB=24m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:28. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )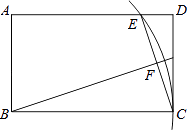 A、 B、 C、 D、9. 若点M(﹣1,y1),N(1,y2),P( )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y1<y2 D、2<y1<y310. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , 按这样的规律进行下去,第2022个正方形(正方形ABCD看作第1个)的面积为( )
A、 B、 C、 D、9. 若点M(﹣1,y1),N(1,y2),P( )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y1<y2 D、2<y1<y310. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , 按这样的规律进行下去,第2022个正方形(正方形ABCD看作第1个)的面积为( )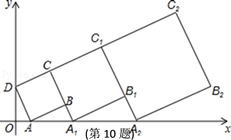 A、5 ( )2020 B、5 ( )2022 C、5 ( )2021 D、5 ( )2022
A、5 ( )2020 B、5 ( )2022 C、5 ( )2021 D、5 ( )2022二、填空题
-
11. 若 = ,则 的值为 .12. 将函数y=﹣2x2的图象沿着x轴向右平移3个单位后所得到的图象的函数表达式为 .13. 14.已知关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是 .14. 如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧弧MN的长度为 .
 15. 小红需要用扇形薄纸板制作成底面半径为9厘米,高为12厘米的圆锥形生日帽,如图所示,则该扇形薄纸板的圆心角为 .
15. 小红需要用扇形薄纸板制作成底面半径为9厘米,高为12厘米的圆锥形生日帽,如图所示,则该扇形薄纸板的圆心角为 . 16. 如图,在△ABC中,∠ACB=90°,AB=9,cosB= ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为.
16. 如图,在△ABC中,∠ACB=90°,AB=9,cosB= ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为. 17. 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为 .
17. 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为 .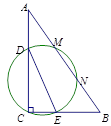
三、解答题
-
18. 解方程:(1)、x2-8x+6=0(2)、2(x-1)2=3x-319. 计算(1)、﹣ +|1﹣4sin60°|;(2)、 .20. 如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).
 (1)、①请在网格图形中画出平面直角坐标系;
(1)、①请在网格图形中画出平面直角坐标系;②以原点O为位似中心,将△ABC放大2倍,画出放大后的△A′B′C′;
③写出△A′B′C′各顶点的坐标,
(2)、写出△A′B′C′的重心坐标.21. 抚顺市某校想知道学生对“遥远的赫图阿拉”,“旗袍故里”等家乡旅游品牌的了解程度,随机抽取了部分学生进行问卷调查,问卷有四个选项(每位被调查的学生必选且只选一项)A.十分了解,B.了解较多,C.了解较少,D.不知道.将调查的结果绘制成如下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题: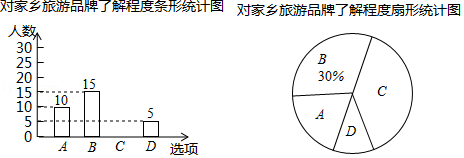 (1)、本次调查了多少名学生?(2)、补全条形统计图;(3)、该校共有500名学生,请你估计“十分了解”的学生有多少名?(4)、在被调查“十分了解”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选两人做家乡旅游品牌宣传员,请用列表或画树状图法求出被选中的两人恰好是一男一女的概率.22. 如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)
(1)、本次调查了多少名学生?(2)、补全条形统计图;(3)、该校共有500名学生,请你估计“十分了解”的学生有多少名?(4)、在被调查“十分了解”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选两人做家乡旅游品牌宣传员,请用列表或画树状图法求出被选中的两人恰好是一男一女的概率.22. 如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)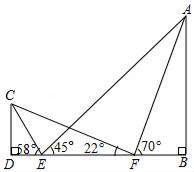 23. 如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
23. 如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.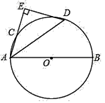 (1)、求证:DE是⊙O的切线;(2)、若∠CAB=60°,DE=3 ,求AC的长.24. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1)、求证:DE是⊙O的切线;(2)、若∠CAB=60°,DE=3 ,求AC的长.24. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.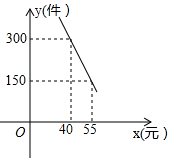 (1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.25. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm .当点Q到达顶点C时,P,Q同时停止运动.设P, Q两点运动时间为t秒.
(1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.25. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm .当点Q到达顶点C时,P,Q同时停止运动.设P, Q两点运动时间为t秒. (1)、当t为何值时,PQ∥BC ?(2)、设四边形PQCB的面积为y,求y关于t的函数解析式;(3)、四边形PQCB的面积与△APQ面积比能为3:2吗?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?26. 如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)、当t为何值时,PQ∥BC ?(2)、设四边形PQCB的面积为y,求y关于t的函数解析式;(3)、四边形PQCB的面积与△APQ面积比能为3:2吗?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?26. 如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点. (1)、求点A的坐标;(2)、求抛物线的解析式;(3)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE= DE.
(1)、求点A的坐标;(2)、求抛物线的解析式;(3)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE= DE.①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
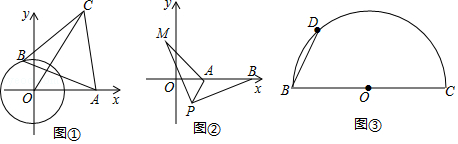
27. (发现问题)爱好数学的小明在做作业时碰到这样的一道题目:如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
 (1)、请你找出图中与OC相等的线段,并说明理由;(2)、求线段OC的最大值.
(1)、请你找出图中与OC相等的线段,并说明理由;(2)、求线段OC的最大值.(灵活运用)
(3)、如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.(迁移拓展)
(4)、如图③,BC=4 ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.