河南省南召县2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1. 下列二次根式中的最简二次根式是( )A、 B、 C、 D、2. 关于 的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根3. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
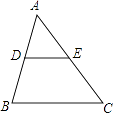 A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:24. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:24. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )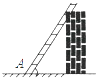 A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关5. 已知 是关于x的一元二次方程 的一个根,则 的值为( )A、 B、 或 C、 或 D、6. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“a是实数,|a|≥0”是不可能事件7. 如图,在△ABC中,点 , 分别在边 , 上,连接 , 交于点 ,且DE∥BC, , , ,则 的长为( )
A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关5. 已知 是关于x的一元二次方程 的一个根,则 的值为( )A、 B、 或 C、 或 D、6. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“a是实数,|a|≥0”是不可能事件7. 如图,在△ABC中,点 , 分别在边 , 上,连接 , 交于点 ,且DE∥BC, , , ,则 的长为( )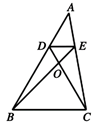 A、 B、 C、 D、8. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: ,则AB的长为
A、 B、 C、 D、8. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: ,则AB的长为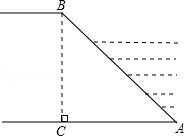 A、12米 B、4 米 C、5 米 D、6 米9. 如果 ,那么锐角 的度数是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )
A、12米 B、4 米 C、5 米 D、6 米9. 如果 ,那么锐角 的度数是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )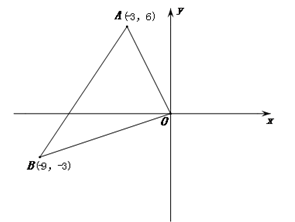 A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)
A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)二、填空题
-
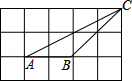
11. 当 时,二次根式 的值是 .12. 一元二次方程x2﹣x=0的根是 .13. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA= .
 14. 从 , , 这三个数字中,随机抽取一个数,记为 ,那么使关于 的一次函数y=2x+a的图象与 轴、 轴围成的三角形的面积为1的概率为 .15. 如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为 .
14. 从 , , 这三个数字中,随机抽取一个数,记为 ,那么使关于 的一次函数y=2x+a的图象与 轴、 轴围成的三角形的面积为1的概率为 .15. 如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为 .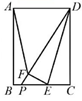
三、解答题
-
16. 先化简,再求值: ,其中 .17. 已知关于 的一元二次方程 .(1)、不解方程,判断方程根的情况;(2)、若该方程的一个实根 时,求 的值.18. 在一个不透明的盒子中放有四张分别写有数字 , , , 的红色卡片和三张分别写有数字 , , 的蓝色卡片,卡片除颜色和数字外完全相同.(1)、从中任意抽取一张卡片,直接写出该卡片上写有数字 的概率为;(2)、将 张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于 的概率.19. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30º,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ≈1.73)
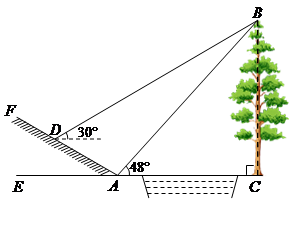 20. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从 年底的 万个增长到 年底的 万个,求该市这两年(从 年底到 年底)拥有的养老床位数的平均年增长率;
20. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从 年底的 万个增长到 年底的 万个,求该市这两年(从 年底到 年底)拥有的养老床位数的平均年增长率;个.
(2)、若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共 间,这三类养老专用房间分别为单人间( 个养老床位),双人间( 个养老床位),三人间( 个养老床位),因实际需要,单人间房间数在 至 之间(包括 和 ),且双人间的房间数是单人间的 倍,设规划建造单人间的房间数为 .①若该养老中心建成后可提供养老床位 个,求 的值;
②直接写出:该养老中心建成后最多提供养老床位多少个;最少提供养老床位多少个.
21. 如图,已知矩形 ,在 上取两点 在 左边),以 为边作等边三角形 ,使顶点 在 上.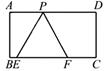
 (1)、求△PEF的边长;(2)、若△PEF的边 在线段 上移动. 分别交 于点 .求证: .22. 如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)、求△PEF的边长;(2)、若△PEF的边 在线段 上移动. 分别交 于点 .求证: .22. 如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.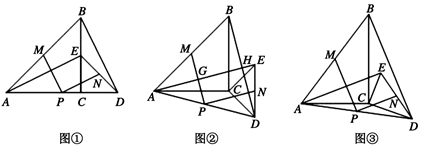 (1)、请直接写出PM与PN的数量关系及位置关系;(2)、现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系;(3)、若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.23. 如图,已知一次函数 与正比例函数 的图象交于点 ,且与 轴交于点 .
(1)、请直接写出PM与PN的数量关系及位置关系;(2)、现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系;(3)、若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.23. 如图,已知一次函数 与正比例函数 的图象交于点 ,且与 轴交于点 .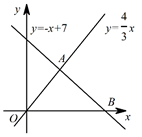 (1)、直接写出点 的坐标为;点 的坐标为;(2)、过点 作 轴于点 ,过点 作直线l∥y轴.动点 从点 出发,以每秒 个单位长的速度,沿 的路线向点 运动;同时直线 从点 出发,以相同速度向左平移,在平移过程中,直线 交 轴于点 ,交线段 或线段 于点 .当点 到达点 时,点 和直线 都停止运动.在运动过程中,设动点 运动的时间为 秒.
(1)、直接写出点 的坐标为;点 的坐标为;(2)、过点 作 轴于点 ,过点 作直线l∥y轴.动点 从点 出发,以每秒 个单位长的速度,沿 的路线向点 运动;同时直线 从点 出发,以相同速度向左平移,在平移过程中,直线 交 轴于点 ,交线段 或线段 于点 .当点 到达点 时,点 和直线 都停止运动.在运动过程中,设动点 运动的时间为 秒.当 为何值时,以 、 、 为顶点的三角形的面积为 ;
是否存在以 、 、 为顶点的三角形是等腰三角形?若存在,直接写出 的值;若不存在,请说明理由.